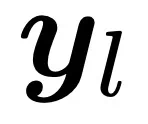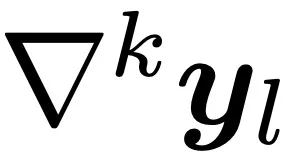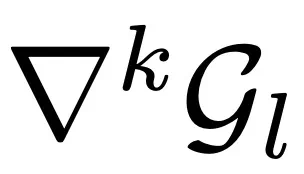文章来源于互联网:NeurIPS 2024 | 数学推理场景下,首个分布外检测研究成果来了

AIxiv专栏是机器之心发布学术、技术内容的栏目。过去数年,机器之心AIxiv专栏接收报道了2000多篇内容,覆盖全球各大高校与企业的顶级实验室,有效促进了学术交流与传播。如果您有优秀的工作想要分享,欢迎投稿或者联系报道。投稿邮箱:liyazhou@jiqizhixin.com;zhaoyunfeng@jiqizhixin.com

-
论文题目:Embedding Trajectory for Out-of-Distribution Detection in Mathematical Reasoning
-
论文地址:https://arxiv.org/abs/2405.14039
-
OpenReview: https://openreview.net/forum?id=hYMxyeyEc5
-
代码仓库:https://github.com/Alsace08/OOD-Math-Reasoning
-
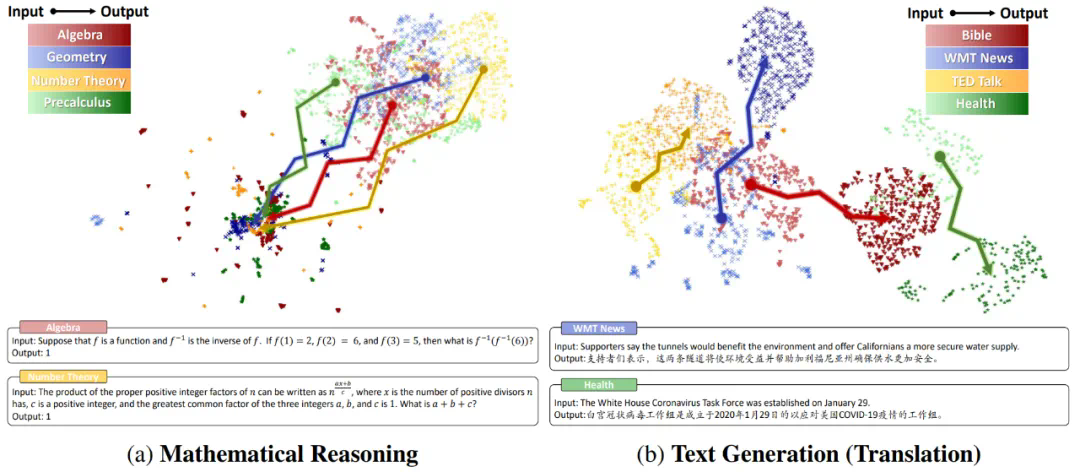
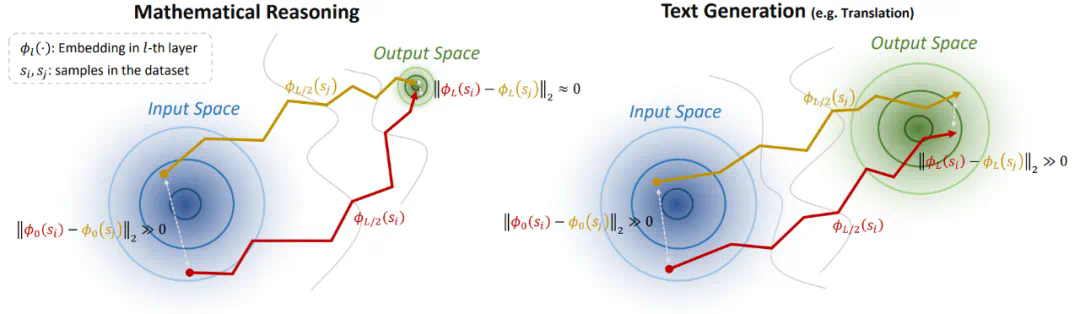
相比于文本生成,数学推理场景下不同域的输入空间的聚类特征并不明显,这意味着 Embedding 可能难以捕获数学问题的复杂度;
-
更重要地,数学推理下的输出空间呈现出高密度叠加特性。研究团队将这种特性称作 “模式坍缩”,它的出现主要有两个原因:
-
(1) 数学推理的输出空间是标量化的,这会增大不同域上的数学问题产生同样答案的可能性。例如 和 这两个问题的结果都等于 4;
-
(2) 语言模型的建模是分词化的,这使得在数学意义上差别很大的表达式在经过分词操作后,共享大量的 token(数字 0-9 和有限的操作符)。研究团队量化了这一观察,其中表示出现的所有 token 数,表示出现过的 token 种类, 表示 token 重复率,表示 token 种类在词表中的占比,发现在一些简单的算术场景下,token 重复率达到了惊人的 99.9%!

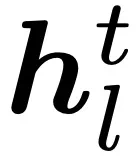 。现将每一层的平均 Embedding
。现将每一层的平均 Embedding 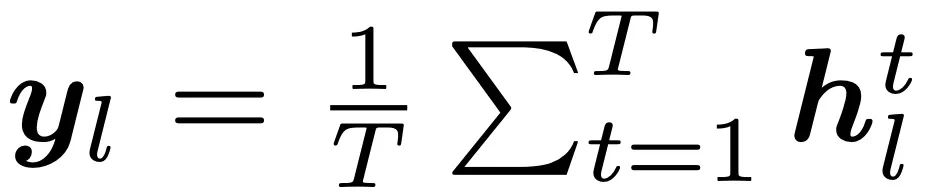 称为第 l 层的句子 Embedding 表征,则动态 Embedding 轨迹可形式化为一个递进的 Embedding 链:
称为第 l 层的句子 Embedding 表征,则动态 Embedding 轨迹可形式化为一个递进的 Embedding 链: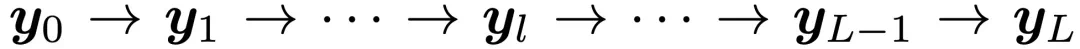
-
理论直觉
-
经验分析
-
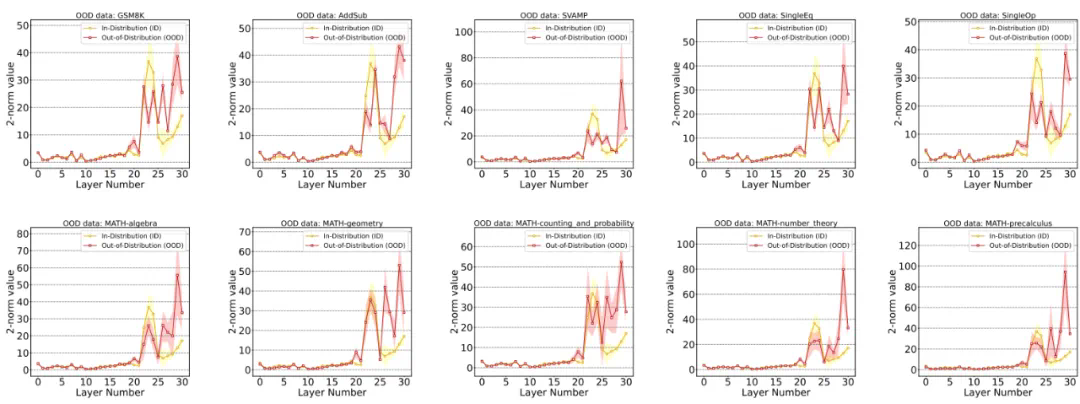
在 20 层之前,ID 和 OOD 样本都几乎没有波动;在 20 层之后,ID 样本的 Embedding 变化幅度先增大后又被逐渐抑制,而 OOD 样本的 Embedding 变化幅度一直保持在相对较高的范围;
-
通过这个观察,可以得出 ID 样本的 “过早稳定” 现象:ID 样本在中后层完成大量的推理过程,而后仅需做简单的适应;而 OOD 样本的推理过程始终没有很好地完成 —— 这意味着 ID 样本的 Embedding 转换相对平滑。
-
首先,将每一层 l 的 ID Embedding 拟合为一个高斯分布:

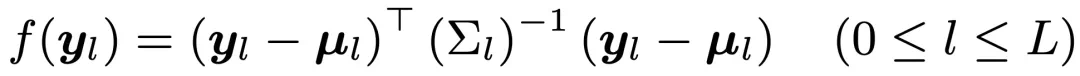
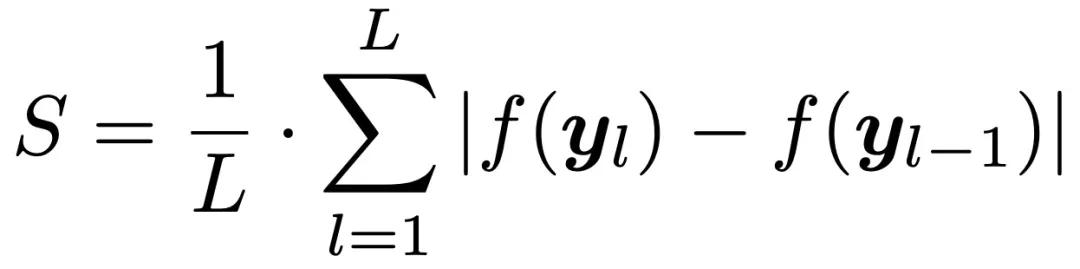
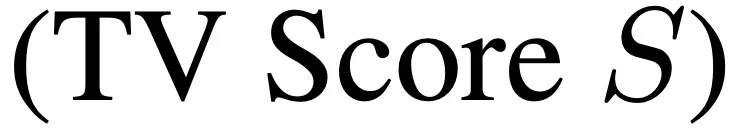
-
首先,定义每一层的 k 阶 Embedding 和高斯分布:
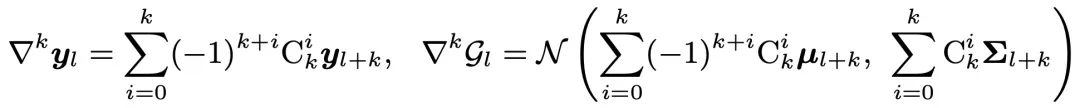
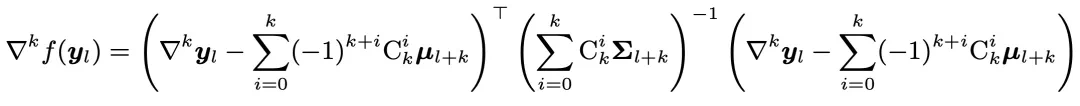
-
最后,类似 TV Score 定义差分平滑后的得分:
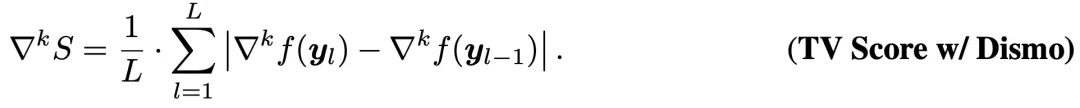
-
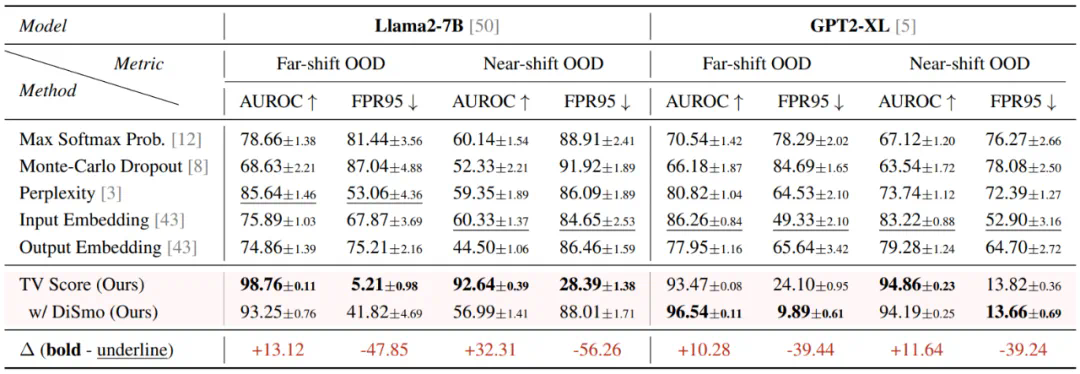
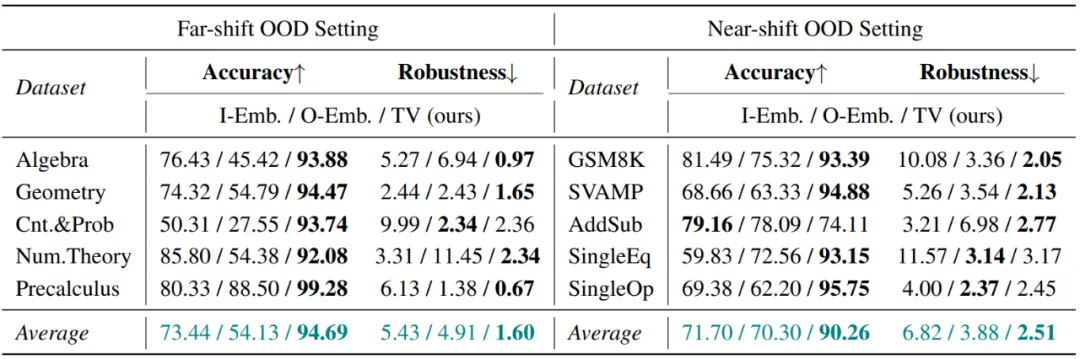
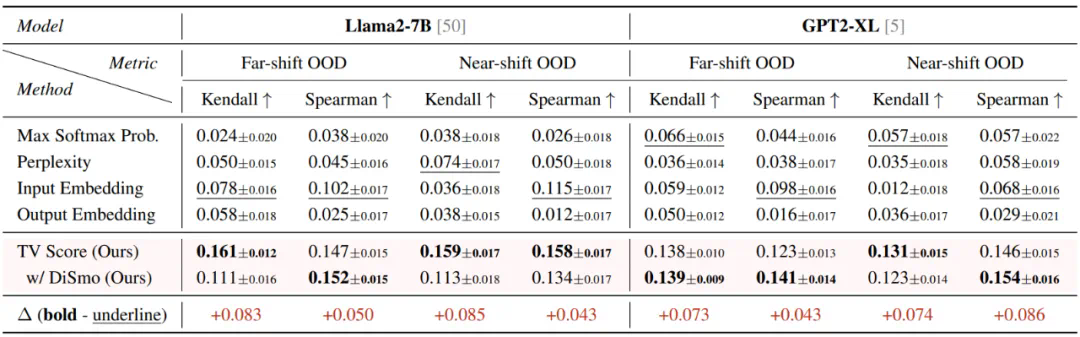
在 Far-shift OOD 场景下:AUROC 指标提高了 10 个点以上,FPR95 指标更是降低了超过 80%;
-
在 Near-shift OOD 场景下:TV Score 展现出更强的鲁棒性。Baseline 方法从 Far-shift 转移到 Near-shift 场景后,性能出现明显下降,而 TV Score 仍然保持卓越的性能。这说明对于更精细的 OOD 检测场景,TV Score 表现出更强的适应性。

文章来源于互联网:NeurIPS 2024 | 数学推理场景下,首个分布外检测研究成果来了