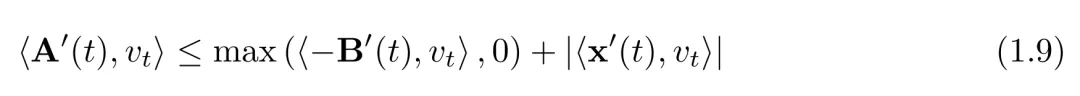文章来源于互联网:困扰数学家近60年的搬沙发难题疑似被解决!119页论文证明最优解,百万网友围观
《老友记》中的罗斯终于能把沙发搬进屋了。

来源:《老友记 S05E16》
该问题是由加拿大数学家 Leo Moser 于 1966 年正式提出:在宽度为 1 的 L 形平面走廊中,能够通过一个直角转弯的「沙发」的最大面积是多少?
1968 年,数学家 John Michael Hammersley 提出了一种简单的解法。他将沙发设计成类似于一个电话听筒的形状,由两个四分之一圆和一个中间的矩形块组成,中间的矩形块中挖去了一个半圆形,从而得出的沙发最大面积为 2.2074。
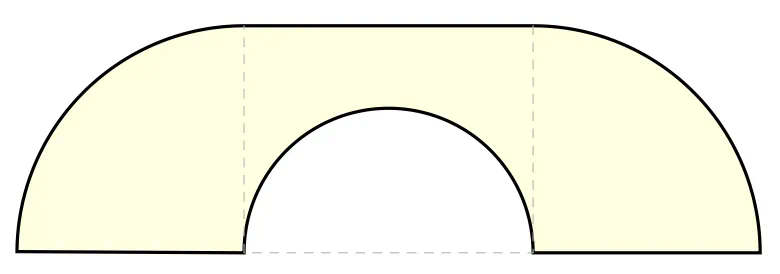
但遗憾的是,这并不是最优解。
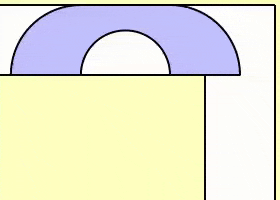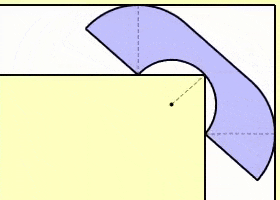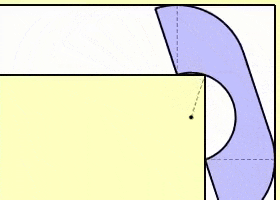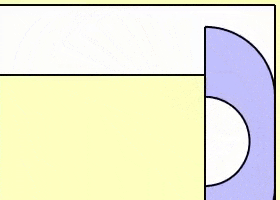
1992 年,美国数学家 Gerver 在 Hammersley 沙发的基础上进行了改进,算出的最大沙发面积为 2.2195,虽然比 Hammersley 沙发面积略大一些,但在方法上却聪明得多。
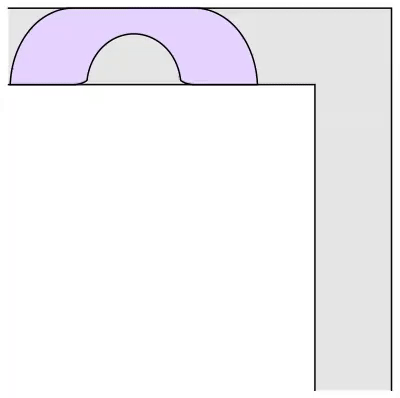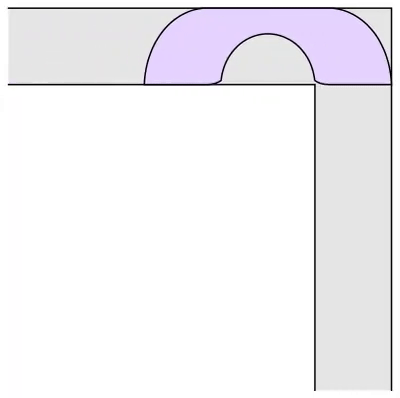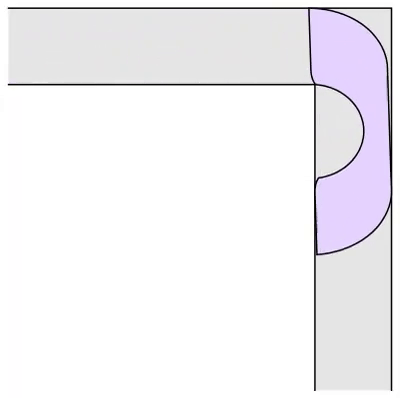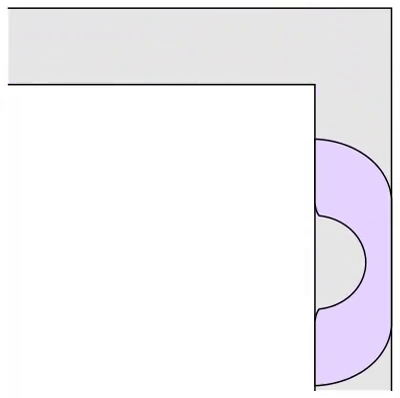
Gerver 沙发由 18 条不同的曲线段组成,其中包括圆弧、圆的渐开线以及圆的渐开线的渐开线等多种曲线。每条曲线段都由一个单独的解析表达式描述,这使得 Gerver 沙发在数学上非常复杂。
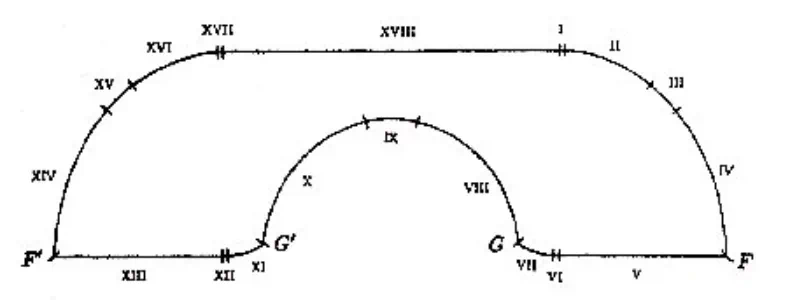
Gerver 推测他的解决方案是最优的,但他无法证明他的沙发是唯一一个(并且是最大面积的)满足这个强条件的沙发。
2024 年 12 月 2 日,韩国学者 Jineon Baek 发表了一篇新论文,声称证明了 Gerver 确实是正确的 —— 他的沙发是最优的。这项研究在社交媒体(如 x)上的热度非常高,引起了很多人的关注。

图源:x@Scientific_Bird
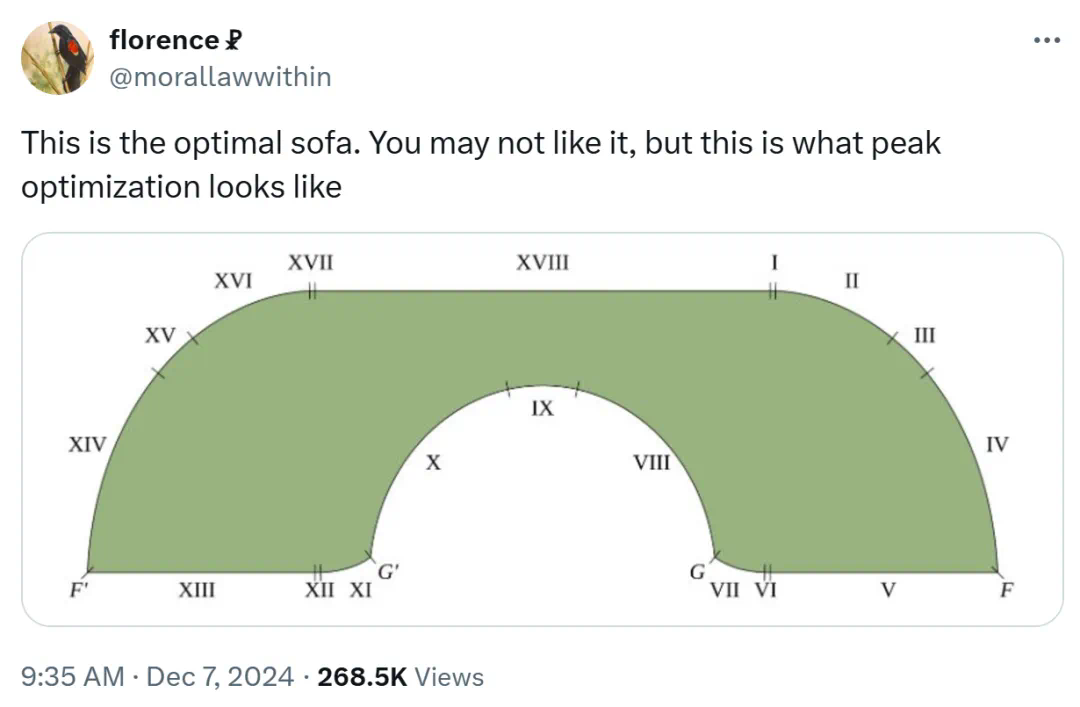
图源:x@morallawwithin
不过,Jineon Baek 的证明论文足足有 119 页,题目为《Optimality of Gerver’s Sofa》。相关专家验证证明的正确性还需要一些时间。

论文地址:https://arxiv.org/pdf/2411.19826
这道困扰人类 58 年的数学难题终于有了答案,不少网友也发表了自己的看法。
「我甚至不是数学家,自从 20 年前听说这个问题后,我就一直在思考它。每次我需要把东西通过门时,我都会想到这个问题。」

「我没想到这个形状会是最优的,这 18 个部分看起来不够优雅。」

证明过程简述
论文共分 8 章,目录如下:


摘要只有一句话,「通过证明具有 18 个曲线段的 Gerver 沙发的确达到了最大面积 2.2195,进而解决了移动沙发问题」。
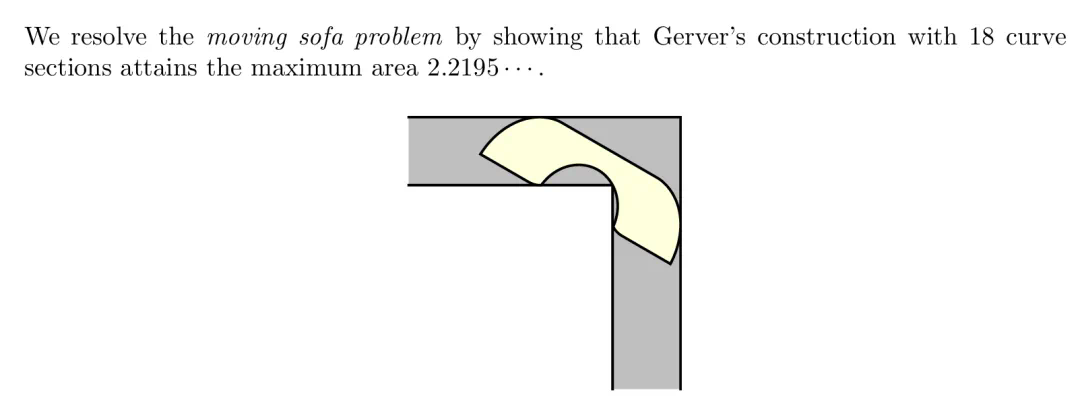
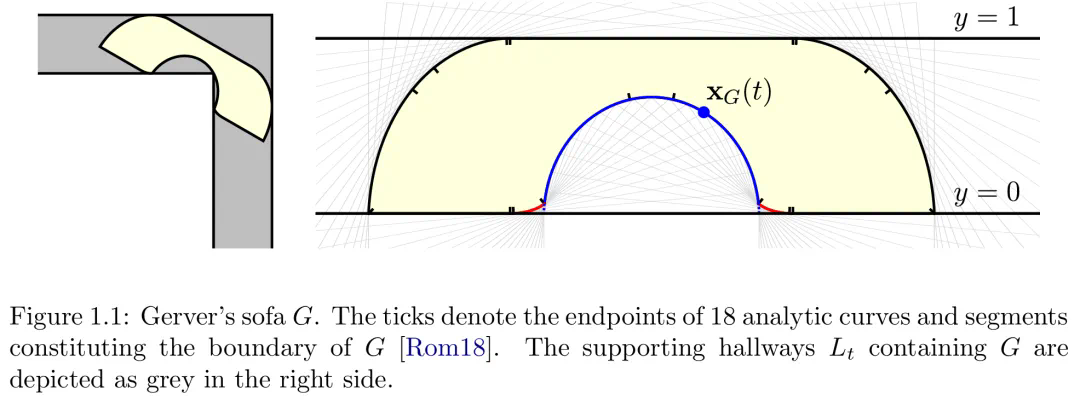
下图为 Gerver 的沙发 G。刻度表示构成 G 边界的 18 条解析曲线和线段的端点,包含 G 的支撑走廊 L_t 在右侧以灰色表示。
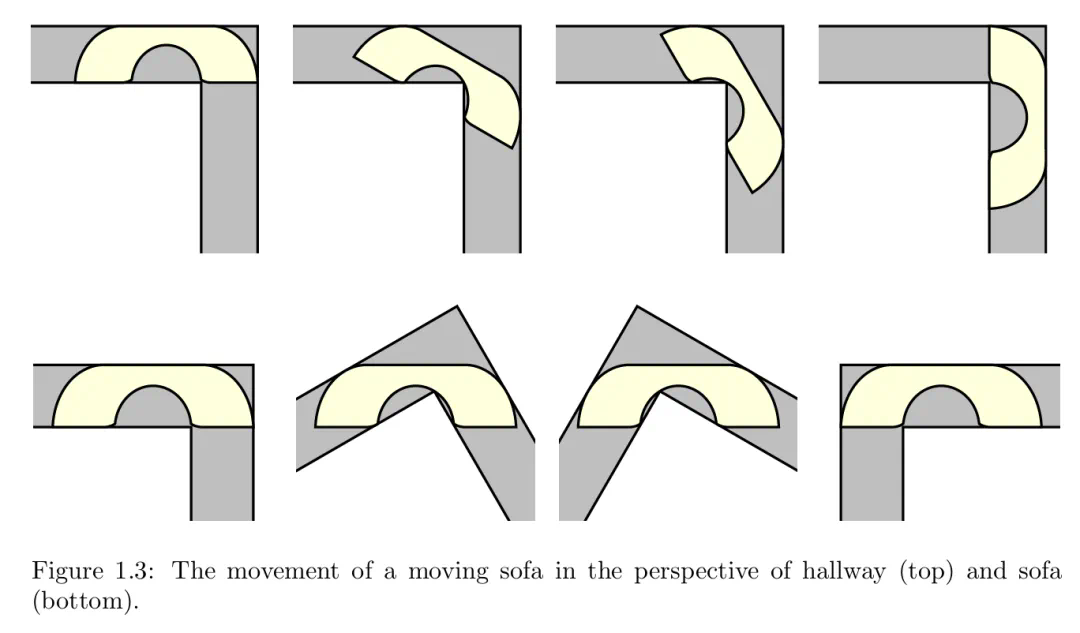
在证明 Gerver 的沙发 G 达到最大面积的过程中,作者除了在科学计算器上进行数值计算之外,没有使用任何的计算机辅助。下图 1.3 为从走廊(顶部)和沙发(底部)视角来看移动沙发的移动。
这个问题之所以很难,是因为没有一个通用的公式可以计算所有可能的移动沙发面积。因此,为了解决这个问题,作者证明了最大面积的移动沙发 S_max 的一个属性,被称为可注入性条件(injectivity condition)。
对于每个满足条件的移动沙发 S,作者将定义一个更大的形状 R,它类似于 Gerver 沙发的形状(下图 1.2)。那么 R 的面积 Q (S) 就是 S 面积的上限,如果是 Gerver 沙发 G,则 Q (S) 与 S 的精确面积相匹配。S 的可注入性条件确保区域 R 的边界形成 Jordan 曲线,从而能够使用格林定理计算 Q (S)。
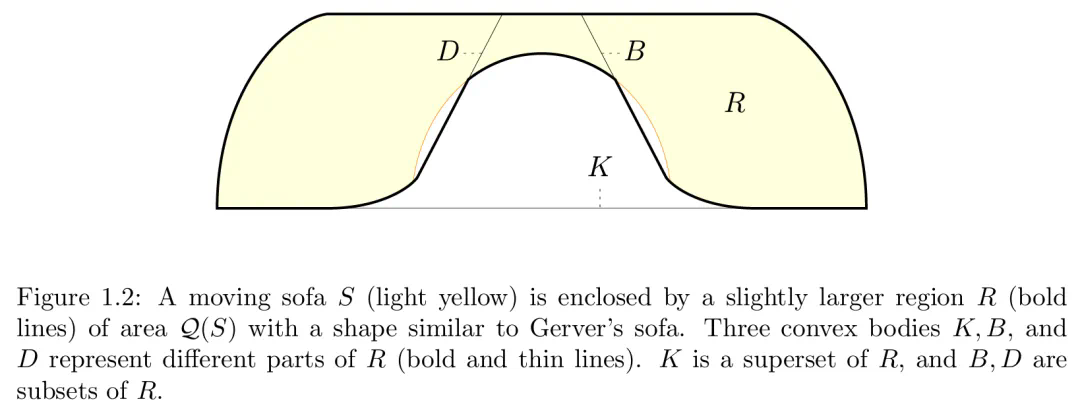
然后,移动沙发 S 面积的上界 Q (S) 相对于 S 的最大值如下所示:作者使用 Brunn-Minkowski 理论将 Q 表示为凸体元组 (K,B,D) 空间 L 上的二次函数(上图 1.2),并使用 Mamikon 定理建立 Q 在 L 上的全局凹性(下图 1.13)。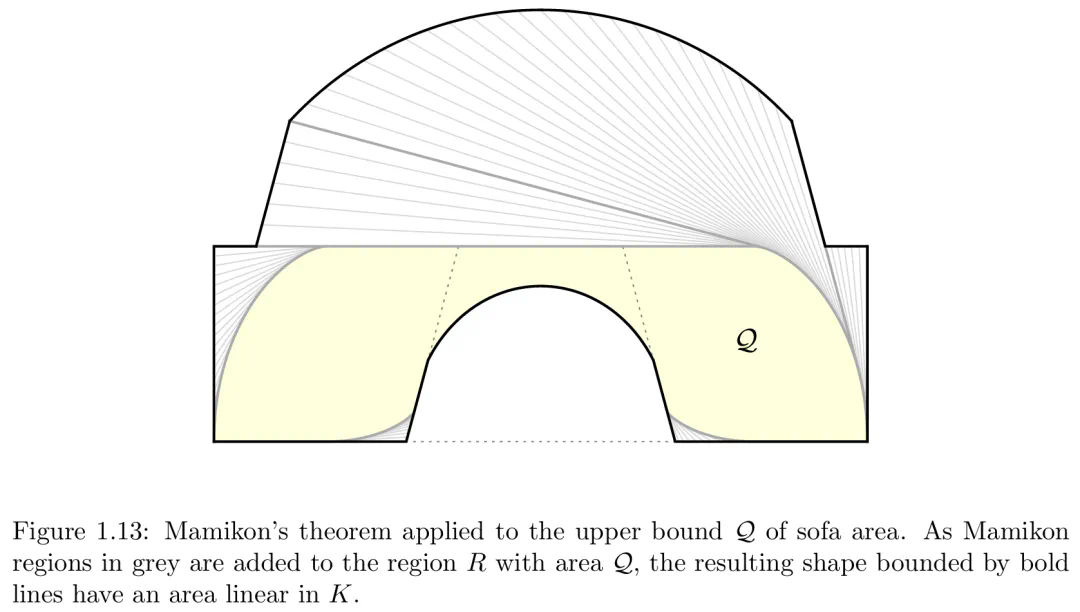
作者使用加州大学戴维斯分校数学系教授 Dan Romik [Rom18] 关于 Gerver 沙发 G 的局部最优方程,来证明 S = G 局部最大化 Q (S)。由于 Q 是凹的,因此 G 也全局最大化 Q。并且,由于上界 Q 与 G 处的面积相匹配,因此沙发 G 也全局最大化了面积,从而证明定理 1.1.1。
具体来讲,定理 1.1.1 的完整证明分为以下三个主要步骤:
-
步骤 1 :限制最大面积移动沙发 S_max 的可能形状;
-
步骤 2 :建立 S_max 的可注入性条件;
-
步骤 3 :构建满足可注入性条件的移动沙发 S 面积的上界 Q (S),并最大化关于 S 的 Q (S)。
其中步骤 1-(a) 将 S_max 的可能形状缩小为单调沙发(monotone sofa),即由支撑走廊内角雕刻出的凹痕的凸体(下图 1.4)。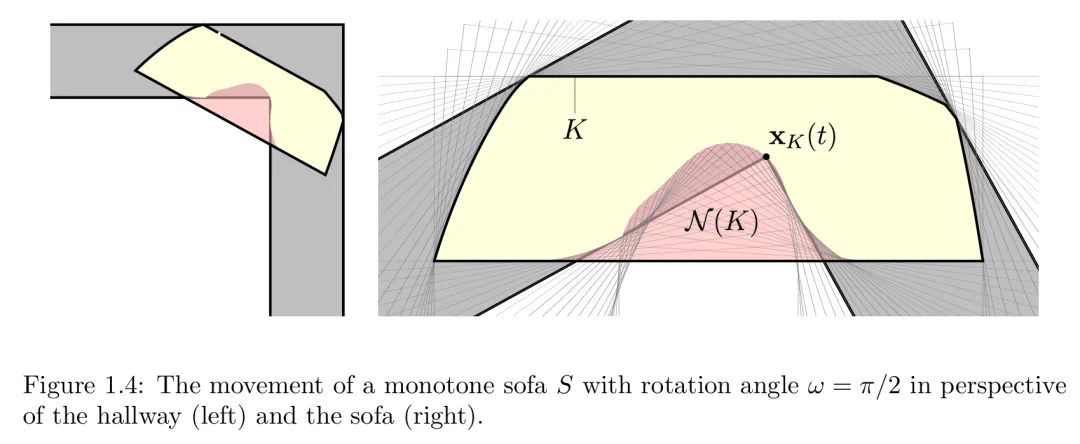
步骤 1-(b) 重新证明了 Gerver 的一个重要局部最优条件,即 S_max 的边长应该相互平衡(定理 1.3.1)。
由于 Gerver 的原始证明存在逻辑漏洞,没有解决移动沙发的连通性问题,因此作者引入了新的想法并重新进行了证明。步骤 1-(c) 使用前面的步骤和基本几何来表明 S_max 在移动过程中旋转了整整一个直角。
步骤 2 证明了 S_max 上的可注入性条件,这是之后建立上限 Q 的关键。它表明 L 内角 (0,0) 的轨迹在移动沙发的视角(参考系)中不会形成自环(下图 1.9)。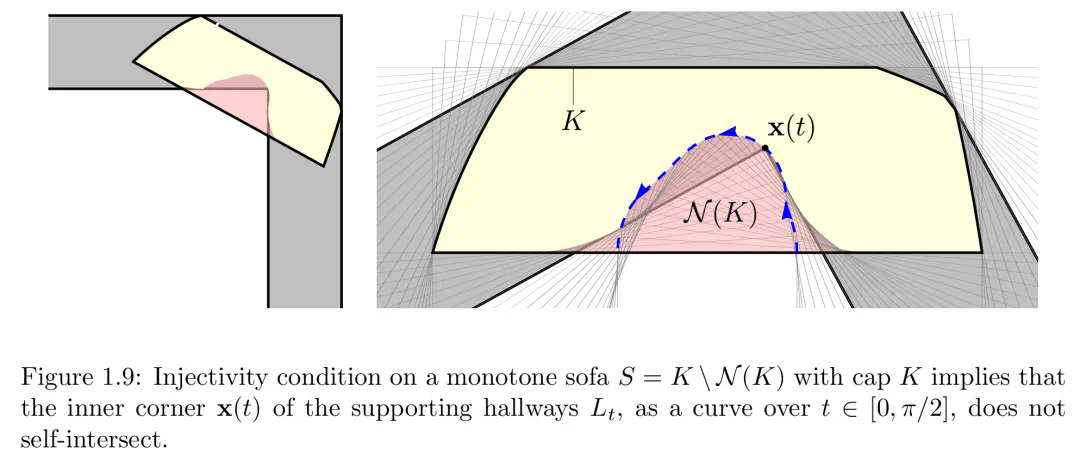
为了证明 S_max 的这一条件,作者在 S_max 上建立了一个新的微分不等式(等式 (1.9)。该不等式受到了 Romik 的一个 ODE 的启发,该 ODE 平衡了 Gerver 沙发的微分边(等式 (1.8))。
步骤 3-(a) 将所有移动沙发的空间 S 扩展为具有单射条件的凸体元组 (K,B,D) 的集合 L,使得每个 S 一一映射到 (K,B,D) ∈ L(但不一定到 L)。该凸体描述了包围 S 的区域 R 的不同部分(上图 1.2)。
步骤 3-(b) 定义了扩展域 L 上的上界 Q。作者遵循 R 的边界,并使用格林定理和 Brunn-Minkowski 理论中关于 K、B 和 D 的二次面积表达式来表示其面积 Q。同时使用单射条件和 Jordan 曲线定理严格证明 Q (K,B,D) 是 S 面积的上界。
步骤 3-(c) 使用 Mamikon 定理确定 Q 在 L 上的凹度(上图 1.13)。步骤 3-(d) 计算由 Gerver 沙发 G 产生的凸体 (K,B,D) ∈ L 处 Q 的方向导数。Romik [Rom18] 在 G 上的局部最优 ODE 用于表明方向导数始终为非正值。这意味着 G 是 Q 在 L 中的局部最优值。Q 在 L 上的凹度意味着 G 也是 Q 在 L 中的全局最优值。由于 G 处 Q 的值与面积匹配,沙发 G 也全局最大化了面积,最终完成定理 1.1.1 的证明。
更具体的证明细节请参考原论文。
作者介绍
这篇论文的作者 Jineon Baek,本科毕业于韩国浦项科技大学,博士期间就读于美国密歇根大学安娜堡分校。现为韩国首尔延世大学的博士后研究员,导师是 Joonkyung Lee。
Jineon Baek2018 年讲解关于非对角线 Erdős-Szekeres 凸多边形问题视频截图
他主要研究兴趣是组合数学和几何学中的优化问题,这类问题往往通过简单却有趣的表述,能够吸引更广泛的受众。
他在人工智能领域也发表过一些相关文章。他在医学图像处理、教育数据挖掘等领域发表了多篇会议和期刊论文,特别是在 X 射线 CT 图像去噪、考试分数预测、标准化考试准备推荐系统等方面有所贡献。
查阅 Jineon Baek 发表过的文章,就会发现这已经不是他第一次研究移动沙发问题了。在今年 6 月他就移动沙发的上限问题进行了研究。在新文章发布的 12 月 2 日当天,arxiv 上显示,这篇论文提交了一个更新版本(v2),之后撤回了该版本。



参考链接:
https://x.com/deedydas/status/1865060166322032764
https://x.com/Scientific_Bird/status/1865116279574528088
https://jcpaik.github.io/CV.pdf