内容目录
文章来源于互联网:扩散模型=流匹配?谷歌DeepMind博客深度详解这种惊人的等价性
扩散模型和流匹配实际上是同一个概念的两种不同表达方式吗?
从表面上看,这两种方法似乎各有侧重:扩散模型专注于通过迭代的方式逐步去除噪声,将数据还原成清晰的样本。
而流匹配则侧重于构建可逆变换系统,目标是学习如何将简单的基础分布精确地映射到真实数据分布。
因为流匹配的公式很简单,并且生成样本的路径很直接,最近越来越受研究者们的欢迎,于是很多人都在问:
「到底是扩散模型好呢?还是流匹配好?」
现在,这个困扰已得到解答。Google DeepMind 的研究团队发现,原来扩散模型和流匹配就像一枚硬币的两面,本质上是等价的 (尤其是在流匹配采用高斯分布作为基础分布时),只是不同的模型设定会导致不同的网络输出和采样方案。
这无疑是个好消息,意味着这两种框架下的方法可以灵活搭配,发挥组合技了。比如在训练完一个流匹配模型后,不必再局限于传统的确定性采样方法,完全可以引入随机采样策略。

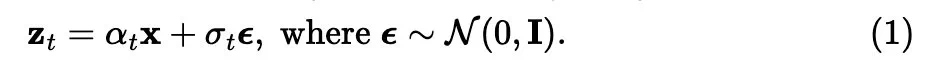
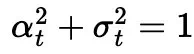 ,称为「方差保持」,意味着在每个时间步骤中,噪声的方差保持不变或接近不变。
,称为「方差保持」,意味着在每个时间步骤中,噪声的方差保持不变或接近不变。 其中,
其中,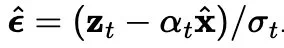

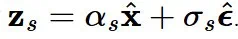 ,有趣的是,重新排列项可以用以下公式来表达,这里涉及几组网络输出和重新参数化:
,有趣的是,重新排列项可以用以下公式来表达,这里涉及几组网络输出和重新参数化: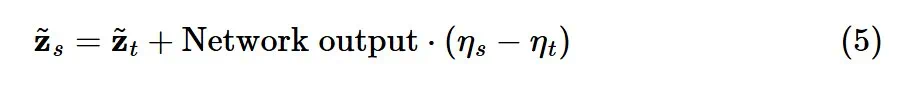
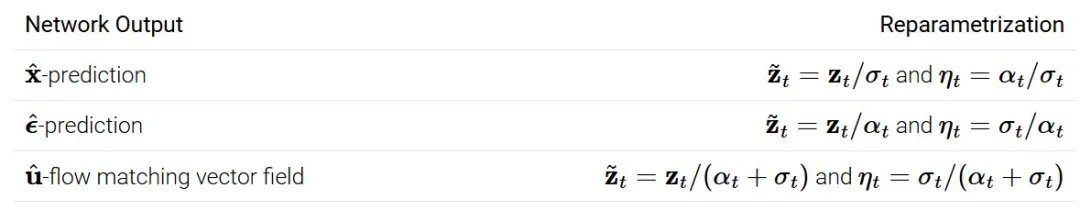
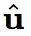 ,并令
,并令 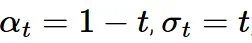 ,可以得到
,可以得到 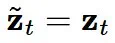 、
、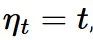 这样我们就恢复了流匹配更新!更准确地说,流匹配更新可以被视为重参数化采样常微分方程(ODE)的欧拉积分:
这样我们就恢复了流匹配更新!更准确地说,流匹配更新可以被视为重参数化采样常微分方程(ODE)的欧拉积分:
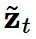 和
和 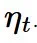 ,这对于其他采样器来说并不成立,例如概率流 ODE 的欧拉采样器。
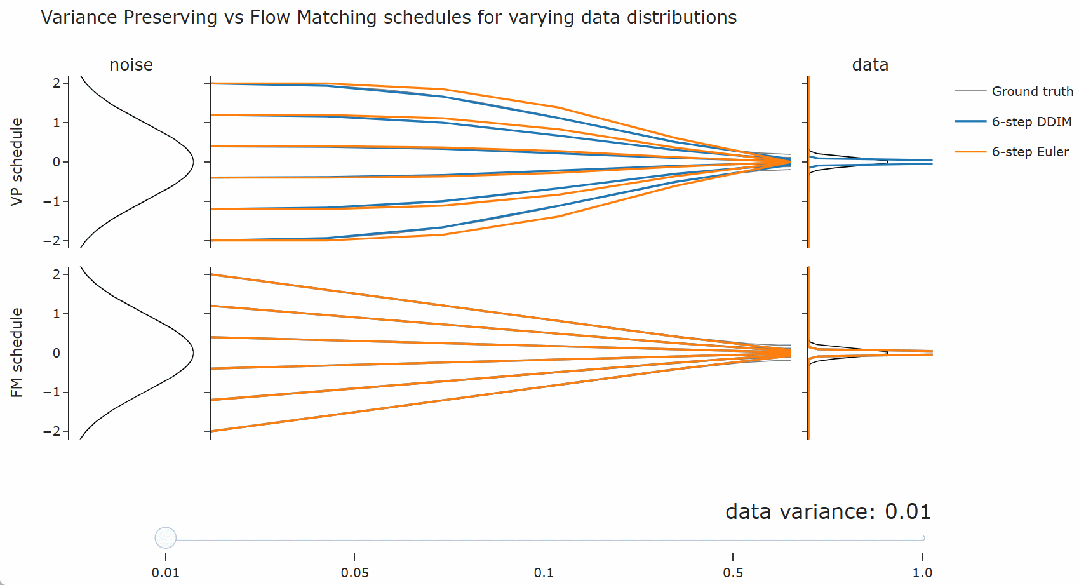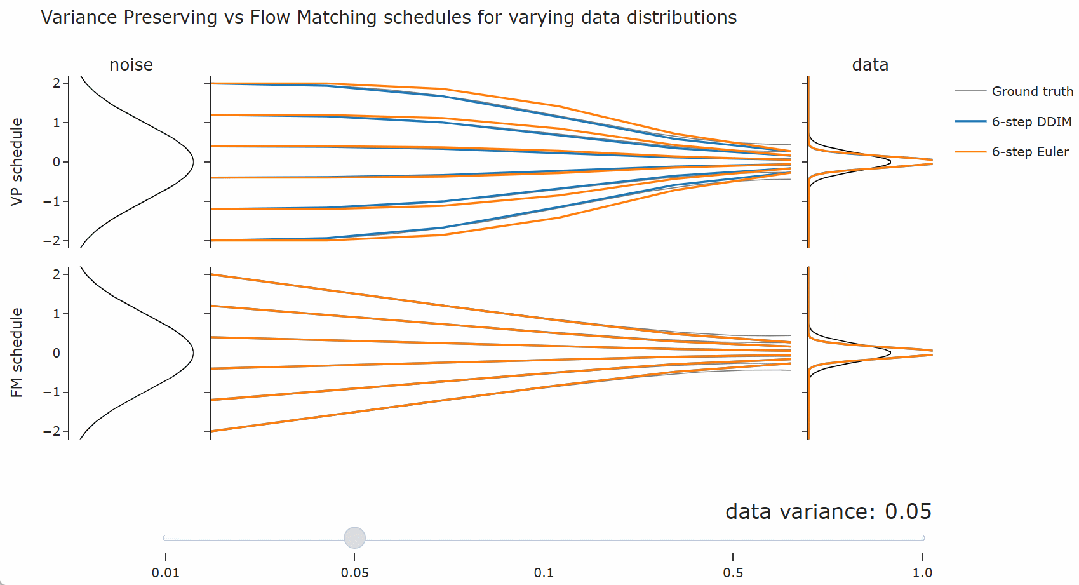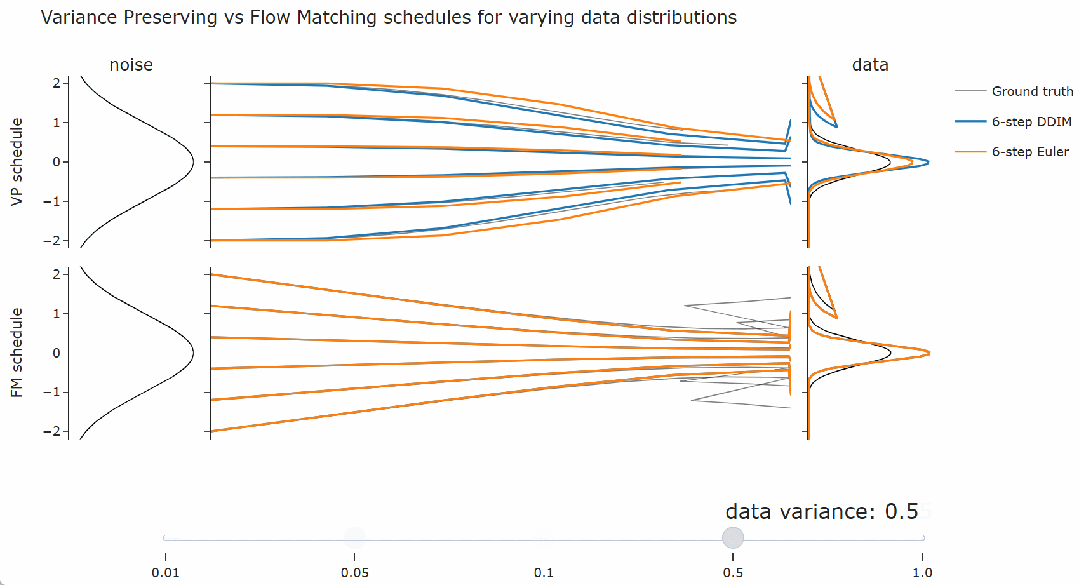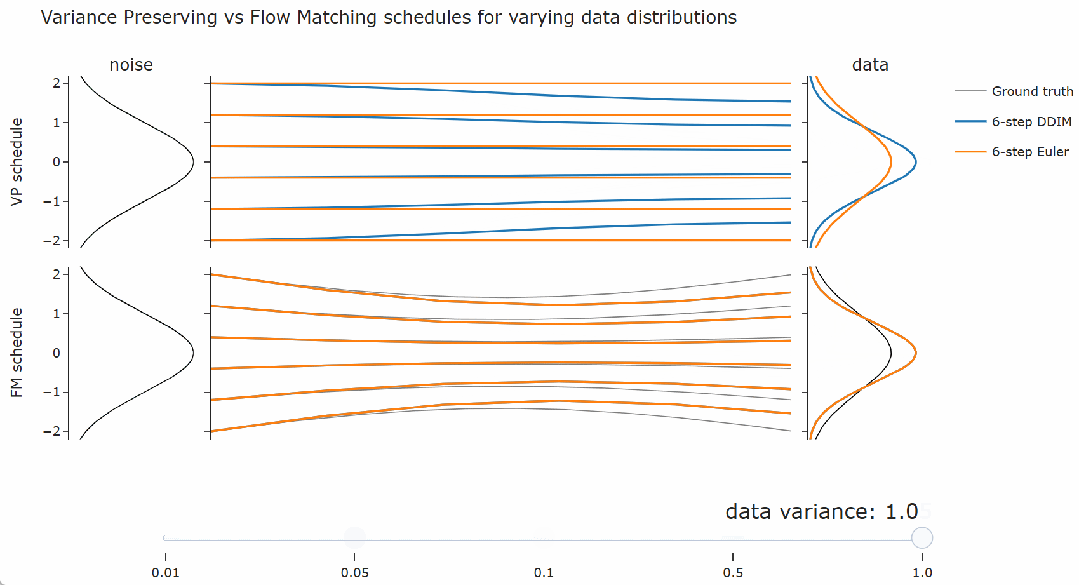
,这对于其他采样器来说并不成立,例如概率流 ODE 的欧拉采样器。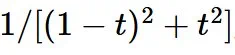 。可以观察到 DDIM(以及流匹配采样器)总是给出相同的最终数据样本,无论调度的缩放如何。对于概率流 ODE 的欧拉采样器,缩放确实会产生真正的差异:可以看到路径和最终样本都发生了变化。
。可以观察到 DDIM(以及流匹配采样器)总是给出相同的最终数据样本,无论调度的缩放如何。对于概率流 ODE 的欧拉采样器,缩放确实会产生真正的差异:可以看到路径和最终样本都发生了变化。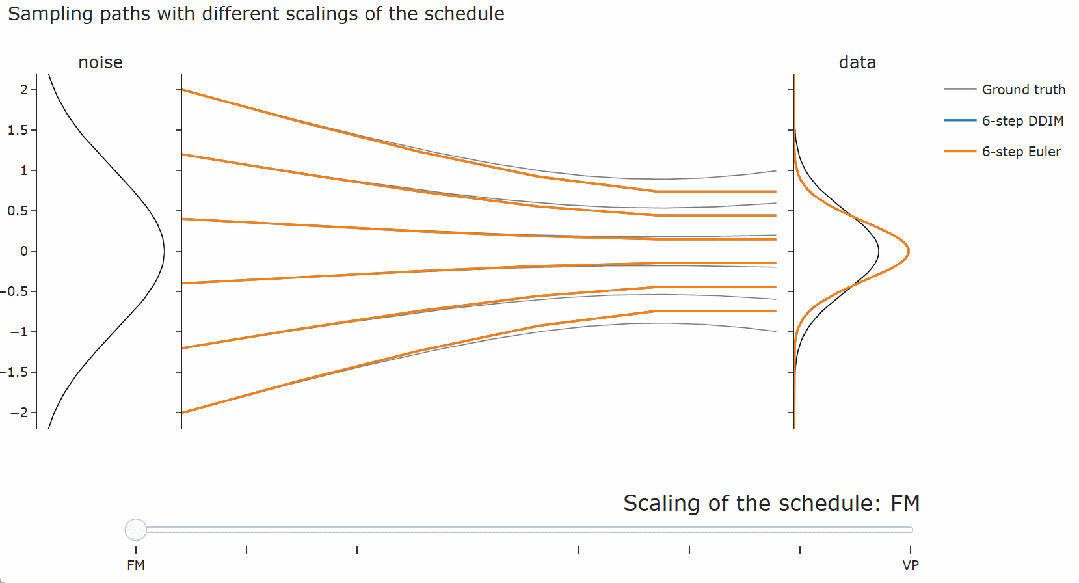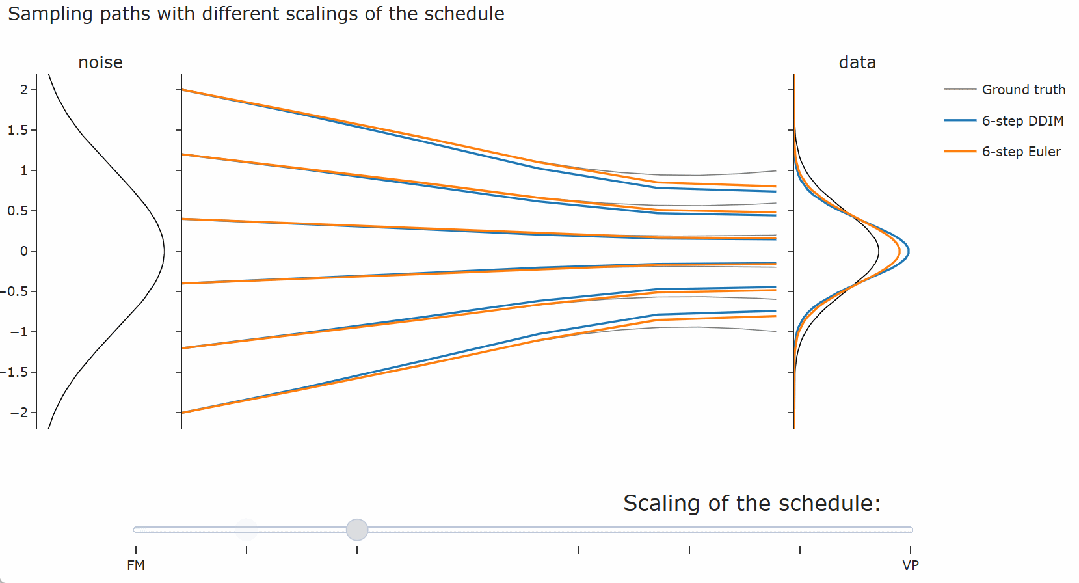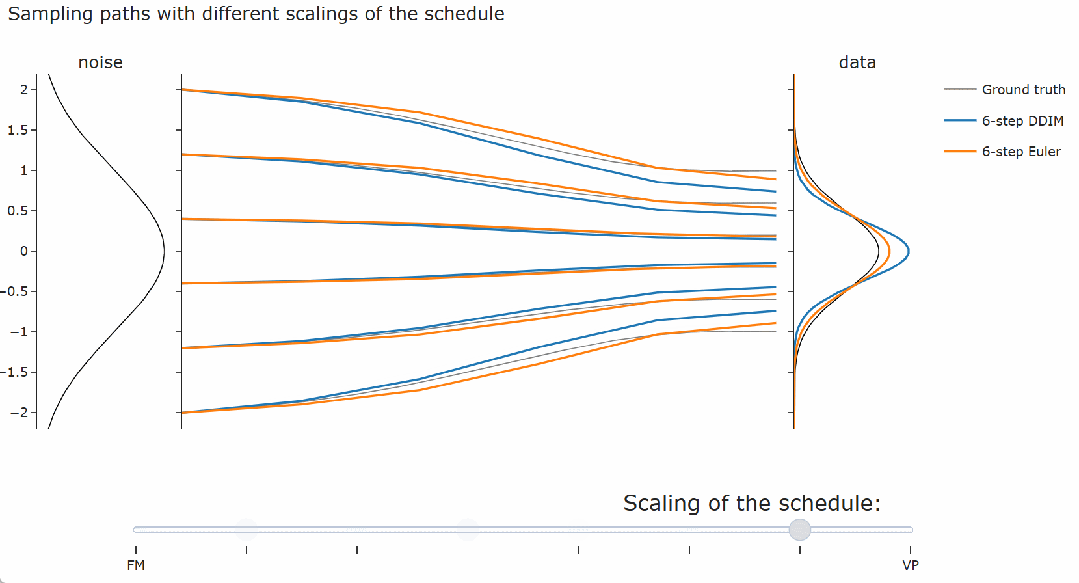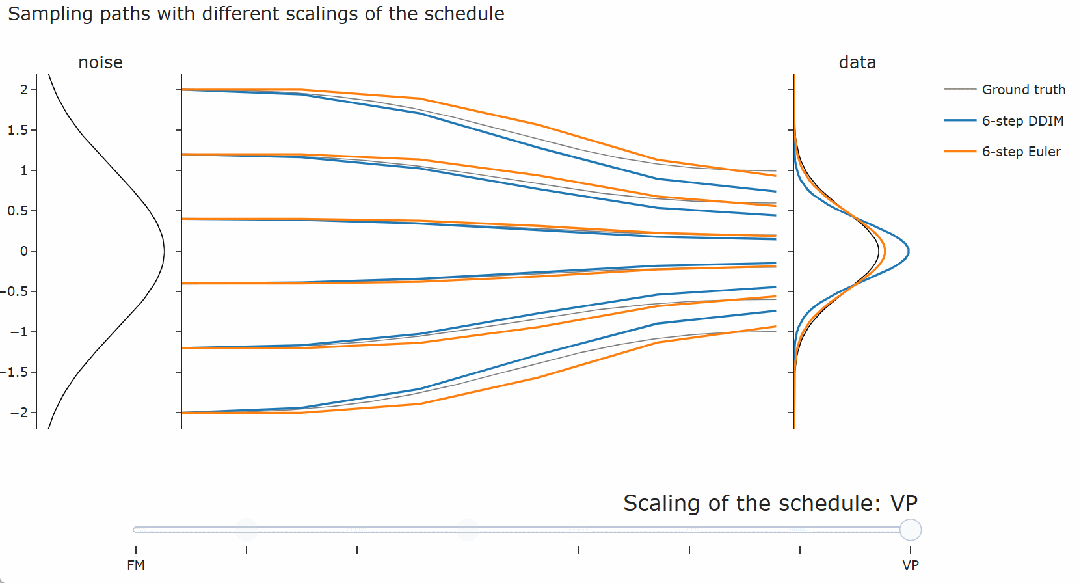
-
采样器的等价性:DDIM 与流匹配采样器等价,并且对噪声调度的线性缩放不变。 -
对直线性的误解:流匹配调度仅在模型预测单个点时才是直线。
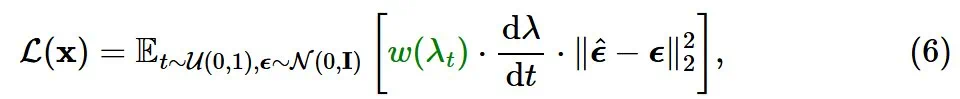
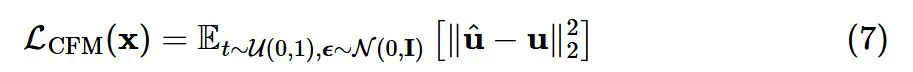

 在低噪声水平下是有问题的,因为
在低噪声水平下是有问题的,因为 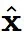 没有信息量,并且错误在
没有信息量,并且错误在 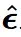 中被放大了。
中被放大了。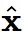 、
、 的组合,这适用于
的组合,这适用于  和流匹配矢量场
和流匹配矢量场 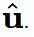

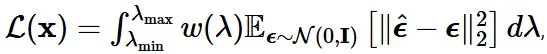 它只与端点(λ_max, λ_min)有关,但与中间的调度 λ_t 无关。在实践中,应该选择合适的 λ_max, λ_min,使得两端分别足够接近干净数据和高斯噪声。λ_t 可能仍然会影响训练损失的蒙特卡洛估计量的方差。一些文献中提出了一些启发式方法来在训练过程中自动调整噪声调度。这篇博文有一个很好的总结:https://sander.ai/2024/06/14/noise-schedules.html#adaptive
它只与端点(λ_max, λ_min)有关,但与中间的调度 λ_t 无关。在实践中,应该选择合适的 λ_max, λ_min,使得两端分别足够接近干净数据和高斯噪声。λ_t 可能仍然会影响训练损失的蒙特卡洛估计量的方差。一些文献中提出了一些启发式方法来在训练过程中自动调整噪声调度。这篇博文有一个很好的总结:https://sander.ai/2024/06/14/noise-schedules.html#adaptive-
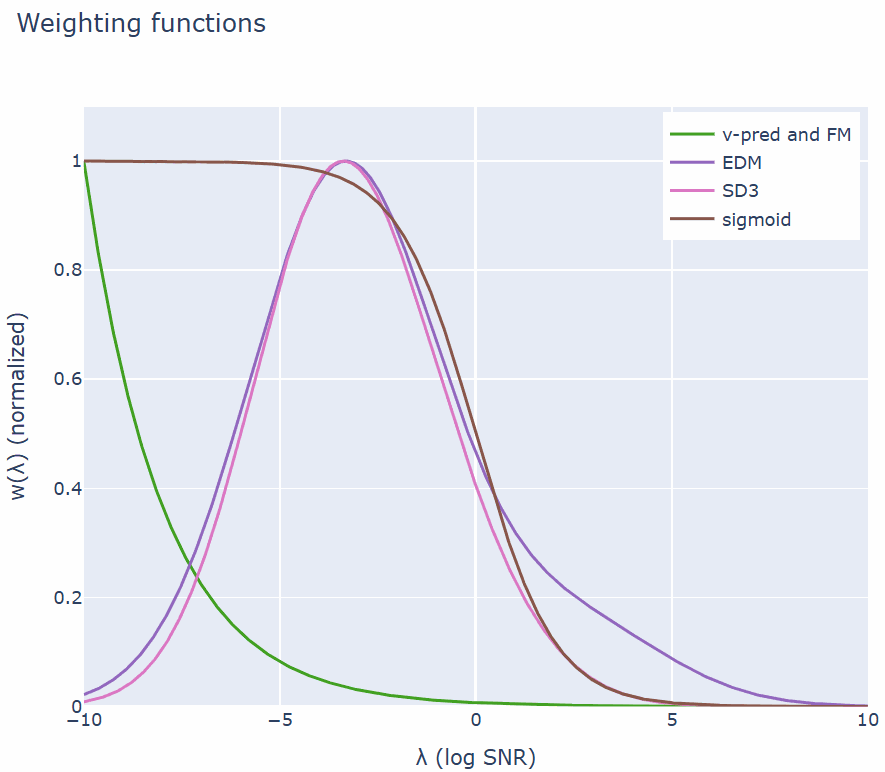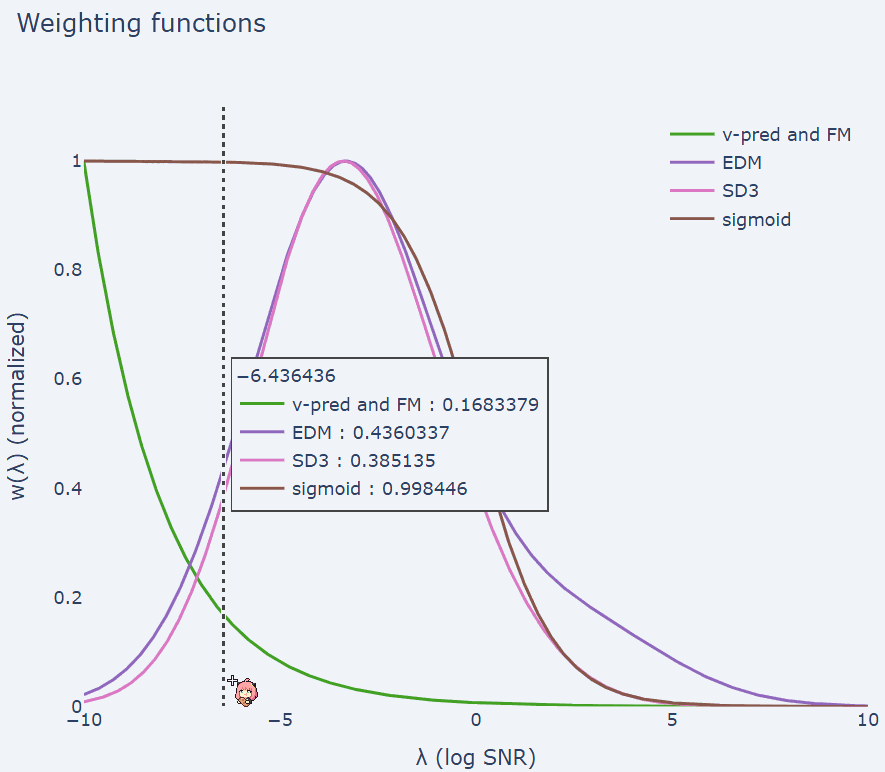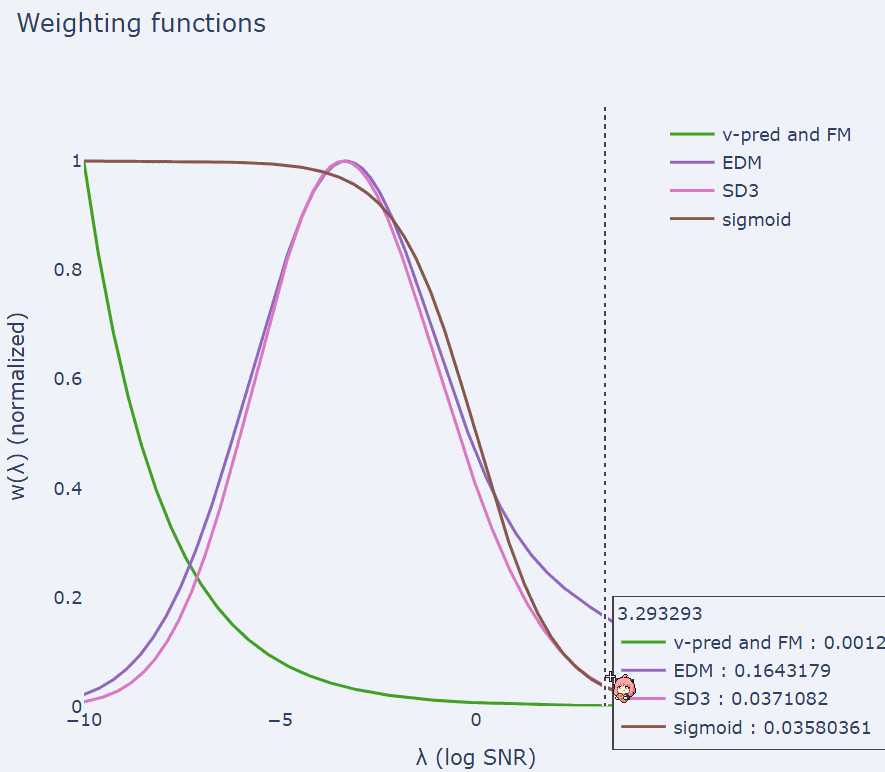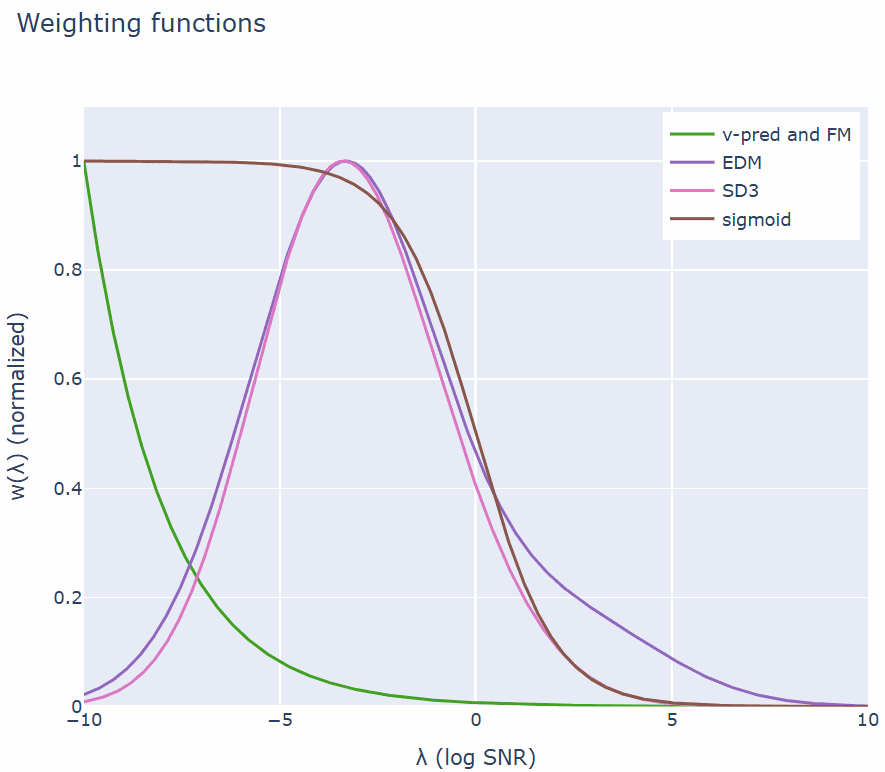
加权中的等价性:加权函数对于训练很重要,它平衡了感知数据不同频率分量的重要性。流匹配加权与常用的扩散训练加权方法相同。 -
训练噪声调度的不重要性:噪声调度对训练目标的重要性要小得多,但会影响训练效率。 -
网络输出的差异:流匹配提出的网络输出是新的,它很好地平衡了 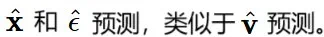
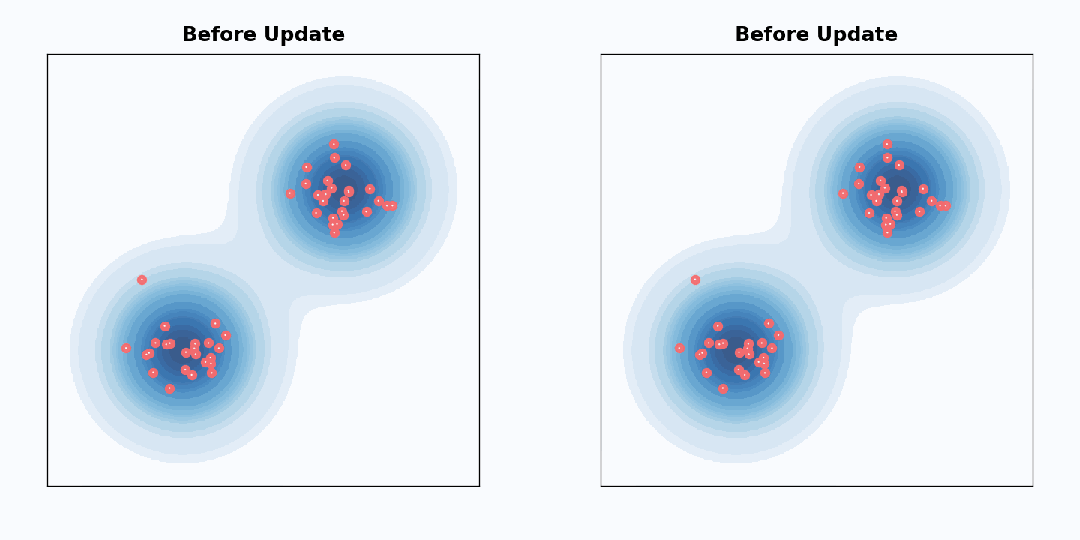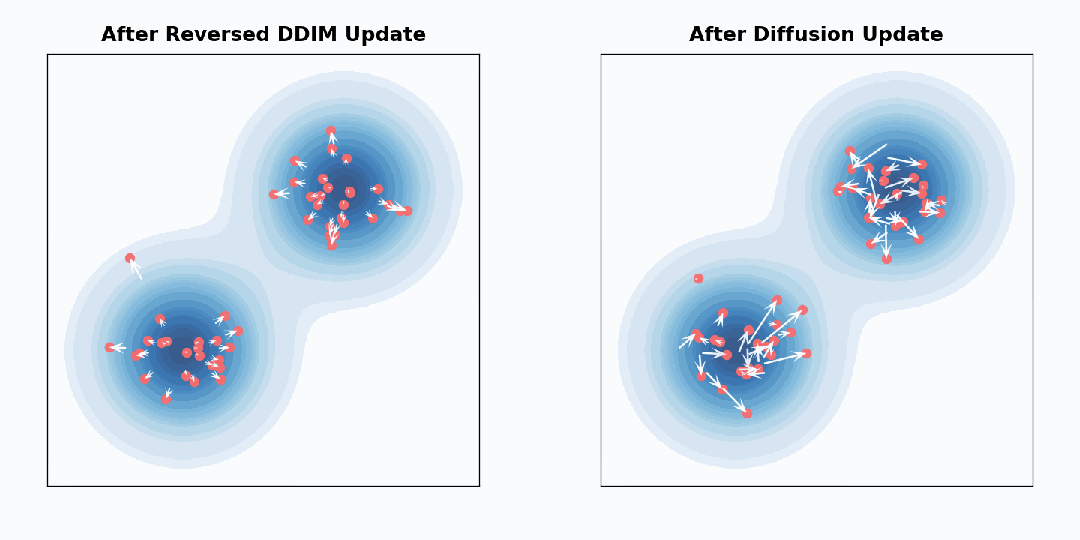
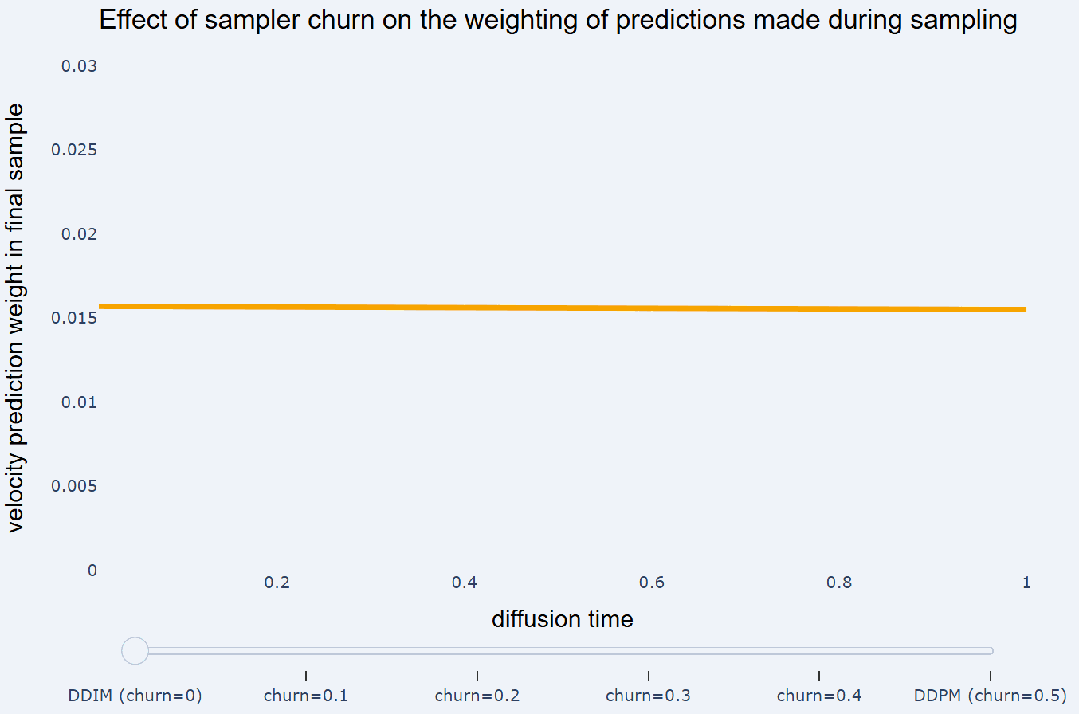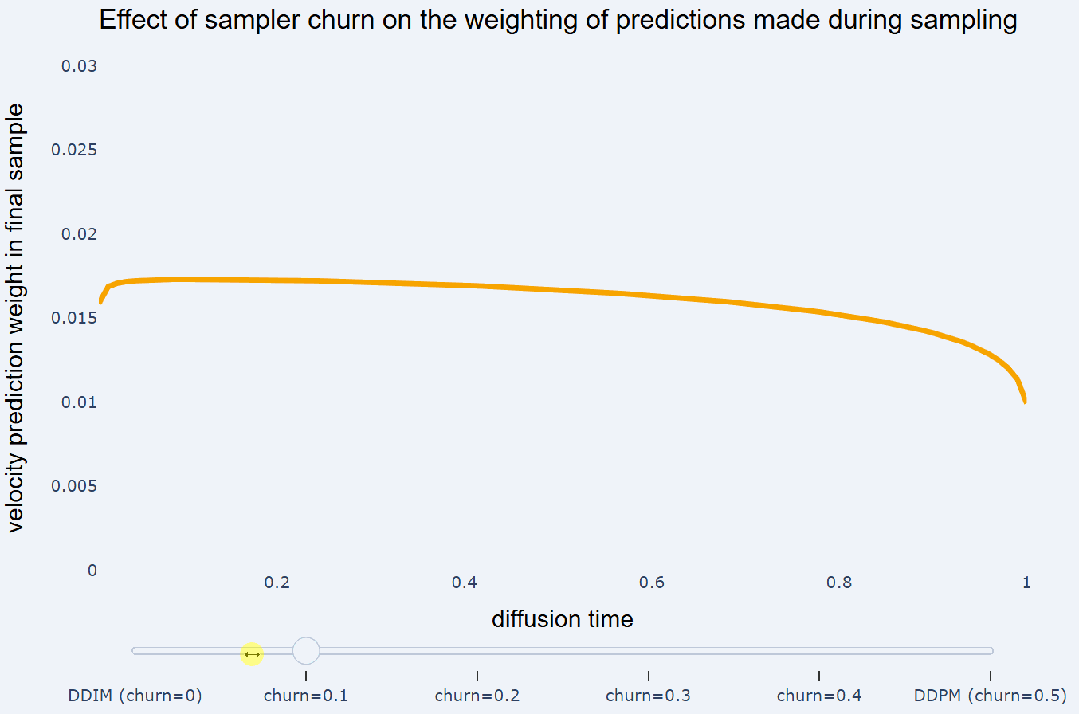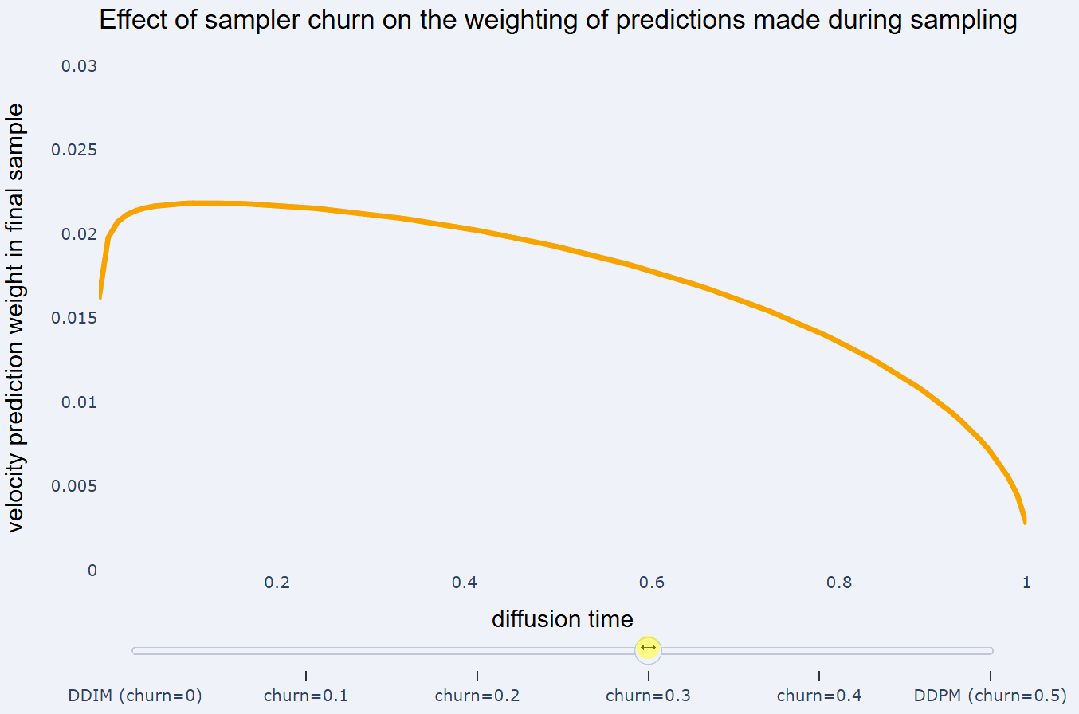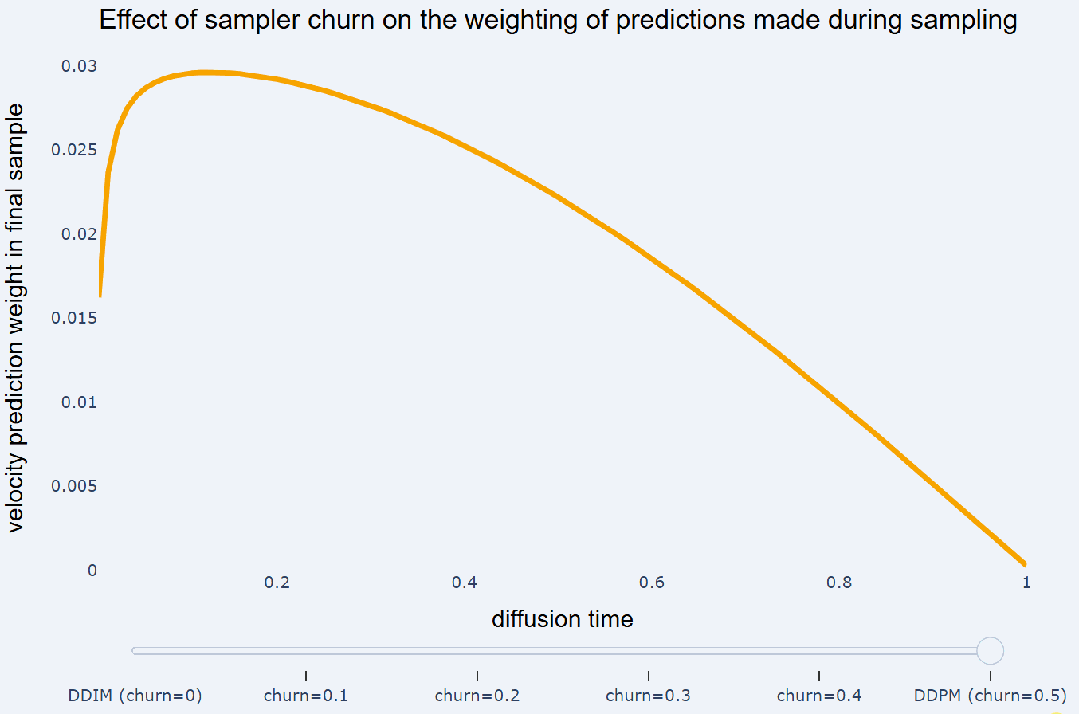
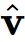 预测将不同采样器都运行了 100 个采样步骤。忽略非线性相互作用,采样器产生的最终样本可以写成采样过程中做出的预测和高斯噪声 e 的加权和:
预测将不同采样器都运行了 100 个采样步骤。忽略非线性相互作用,采样器产生的最终样本可以写成采样过程中做出的预测和高斯噪声 e 的加权和: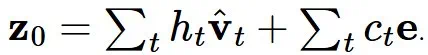
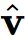 预测赋予相等的权重,而 DDPM 则更注重在采样结束时所做的预测。另请参阅《Dpm-solver++: Fast solver for guided sampling of diffusion probabilistic models》以了解
预测赋予相等的权重,而 DDPM 则更注重在采样结束时所做的预测。另请参阅《Dpm-solver++: Fast solver for guided sampling of diffusion probabilistic models》以了解 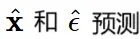 中这些权重的解析表达式。
中这些权重的解析表达式。
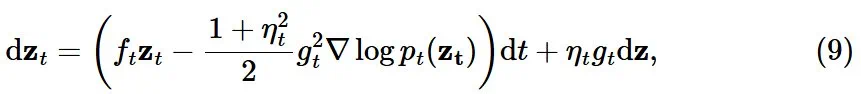


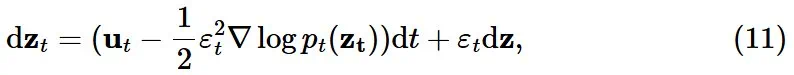
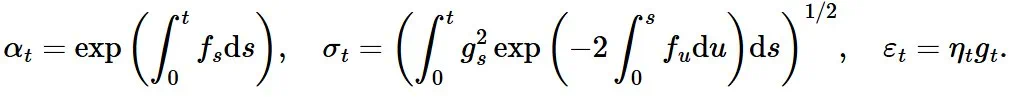
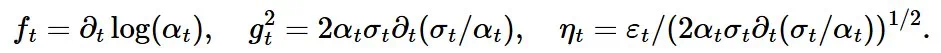
-
网络输出:流匹配提出了一种网络输出的向量场参数化方案,并且其不同于扩散文献中使用的方案。当使用高阶采样器时,网络输出可能会有所不同。它也可能影响训练动态。 -
采样噪声调度:流匹配利用了简单的采样噪声调度 α_t = 1-t 和 σ_t = t,并且更新规则与 DDIM 相同。
-
Flow matching for generative modeling -
Lipman, Y., Chen, R.T., Ben-Hamu, H., Nickel, M. and Le, M., 2022. arXiv preprint arXiv:2210.02747. -
Flow straight and fast: Learning to generate and transfer data with rectified flow -
Liu, X., Gong, C. and Liu, Q., 2022. arXiv preprint arXiv:2209.03003. -
Building normalizing flows with stochastic interpolants -
Albergo, M.S. and Vanden-Eijnden, E., 2022. arXiv preprint arXiv:2209.15571. -
Stochastic interpolants: A unifying framework for flows and diffusions -
Albergo, M.S., Boffi, N.M. and Vanden-Eijnden, E., 2023. arXiv preprint arXiv:2303.08797. -
Denoising diffusion implicit models -
Song, J., Meng, C. and Ermon, S., 2020. arXiv preprint arXiv:2010.02502. -
Score-based generative modeling through stochastic differential equations -
Song, Y., Sohl-Dickstein, J., Kingma, D.P., Kumar, A., Ermon, S. and Poole, B., 2020. arXiv preprint arXiv:2011.13456. -
Understanding diffusion objectives as the elbo with simple data augmentation -
Kingma, D. and Gao, R., 2024. Advances in Neural Information Processing Systems, Vol 36. -
Diffusion is spectral autoregression [HTML] -
Dieleman, S., 2024. -
Scaling rectified flow transformers for high-resolution image synthesis -
Esser, P., Kulal, S., Blattmann, A., Entezari, R., Muller, J., Saini, H., Levi, Y., Lorenz, D., Sauer, A., Boesel, F. and others,, 2024. Forty-first International Conference on Machine Learning. -
Elucidating the design space of diffusion-based generative models -
Karras, T., Aittala, M., Aila, T. and Laine, S., 2022. Advances in neural information processing systems, Vol 35, pp. 26565—26577. -
Knowledge distillation in iterative generative models for improved sampling speed [PDF] -
Luhman, E. and Luhman, T., 2021. arXiv preprint arXiv:2101.02388. -
Denoising diffusion probabilistic models -
Ho, J., Jain, A. and Abbeel, P., 2020. Advances in neural information processing systems, Vol 33, pp. 6840—6851. -
Progressive Distillation for Fast Sampling of Diffusion Models -
Salimans, T. and Ho, J., 2022. International Conference on Learning Representations. -
Dpm-solver++: Fast solver for guided sampling of diffusion probabilistic models -
Lu, C., Zhou, Y., Bao, F., Chen, J., Li, C. and Zhu, J., 2022. arXiv preprint arXiv:2211.01095.
文章来源于互联网:扩散模型=流匹配?谷歌DeepMind博客深度详解这种惊人的等价性


