Search
内容目录

数据科学基础

科学计算神器之一Numpy的使用

矩阵的基本操作(使用Numpy)

import numpy as np

# 快速构建矩阵
matrix = np.array([[1, 2, 3], [4, 5, 6]])

print("矩阵数据：", matrix)

# 查看矩阵的维度信息
print("矩阵维度：", matrix.ndim)

# 查看矩阵的形状
print("矩阵形状：", matrix.shape)

# 查看矩阵的size
print("矩阵size：", matrix.size)

# 对矩阵进行reshape为一个矩阵
reshaped_matrix = matrix.reshape(3, 2)
print("重塑后的矩阵：\n", reshaped_matrix)

# 修改矩阵中的数据内容
matrix[0, 1] = 10
print("修改后的矩阵：\n", matrix)

# 将矩阵的数据类型转换
matrix = matrix.astype(float)
print("转换数据类型后的矩阵：\n", matrix)

# 随机生成一个新的矩阵
new_matrix = np.random.rand(2, 3)
print("随机生成的新矩阵：\n", new_matrix)

矩阵的生成(使用Numpy)

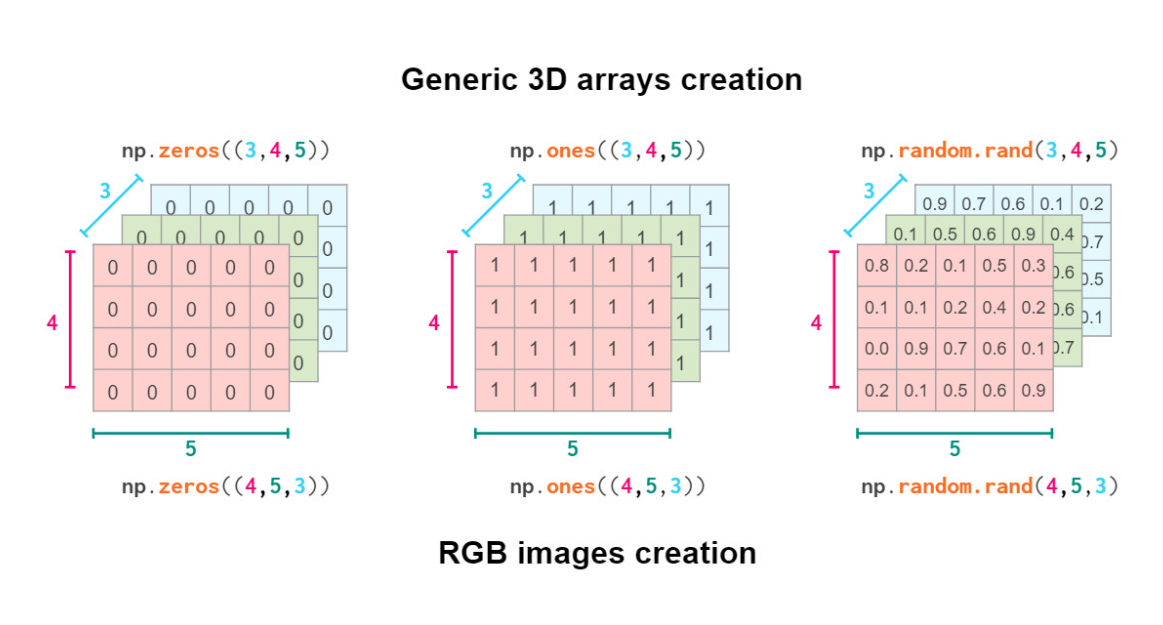
# 生成一个形状为 (3, 4, 5) 的数组,内容都为0
arry_zero = np.zeros((3, 4, 5))
print(arry_zero)

# 生成一个形状为 (3, 4, 5) 的数组,内容都为1
array_ones = np.ones((3, 4, 5))
print(array_ones)

# 生成一个形状为 (3, 4, 5) 的数组，内容为随机
array_random = np.random.rand(3, 4, 5)
print(array_random)

矩阵的堆叠和拼接(使用Numpy)

在 NumPy 中，np.concatenate、np.stack、np.vstack、np.hstack 和 np.dstack 是用于数组堆叠和连接的函数，它们之间有一些区别和联系：

  • np.concatenate：
    • np.concatenate 是一个通用的函数，用于沿指定轴连接数组。
    • 可以在指定的轴（axis）上连接两个或多个数组。
    • 可以控制连接的方向，例如沿行（axis=0）或列（axis=1）进行连接。
  • np.stack：
    • np.stack 是用于沿新轴（堆叠轴）堆叠数组的函数。
    • 创建一个新轴来堆叠数组，改变数组的维度。
    • 可以通过 axis 参数控制在哪个位置添加新轴。
  • np.vstack：
    • np.vstack 是用于垂直（沿着行方向）堆叠数组的函数。
    • 将两个或多个数组按行堆叠在一起。
  • np.hstack：
    • np.hstack 是用于水平（沿着列方向）堆叠数组的函数。
    • 将两个或多个数组按列堆叠在一起。
  • np.dstack：
    • np.dstack 是用于深度（沿着第三维）堆叠数组的函数。
    • 将两个或多个数组按深度方向堆叠在一起。
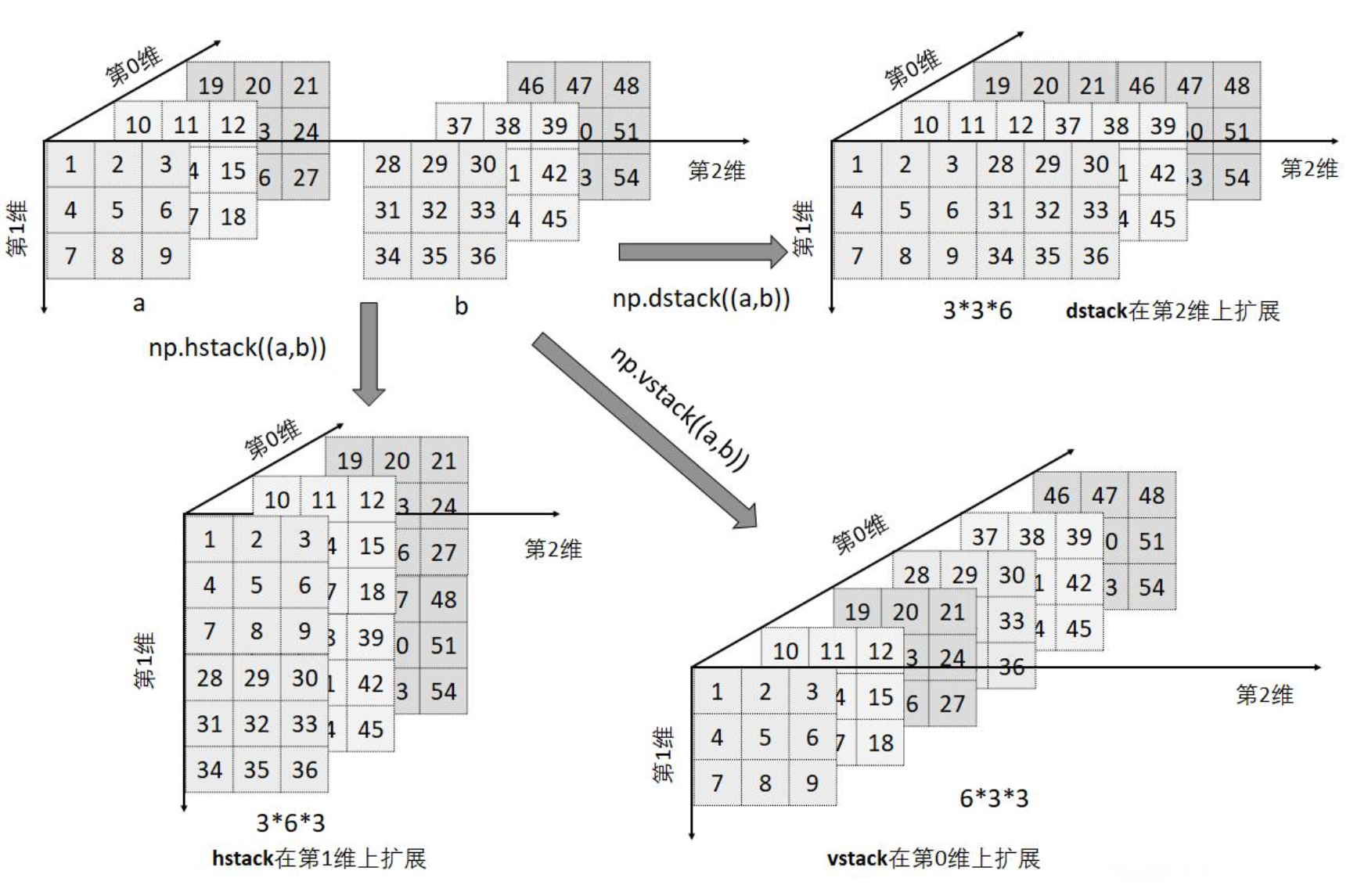
np.concatenate和np.stack
import numpy as np

a = np.arange(1, 28).reshape(3, 3, 3)
b = np.arange(28, 55).reshape(3, 3, 3)

#  np.dstack((a, b))与 np.concatenate((a, b), axis=2) 效果一样
print("np.dstack((a, b))：", np.dstack((a, b)))
print("np.concatenate((a, b), axis=2)：", np.concatenate((a, b), axis=2))

#  np.hstack((a, b))与 np.concatenate((a, b), axis=1) 效果一样
print("np.hstack((a, b))：", np.hstack((a, b)))
print("np.concatenate((a, b), axis=1)：", np.concatenate((a, b), axis=1))

#  np.vstack((a, b))与 np.concatenate((a, b), axis=0) 效果一样
print("np.vstack((a, b))：", np.vstack((a, b)))
print("np.concatenate((a, b), axis=0)：", np.concatenate((a, b), axis=0))

在Numpy进行数据处理时，需要掌握维度的概念：

  • 按维度定义数据
  • 按维度读取数据
  • 按维度处理数据
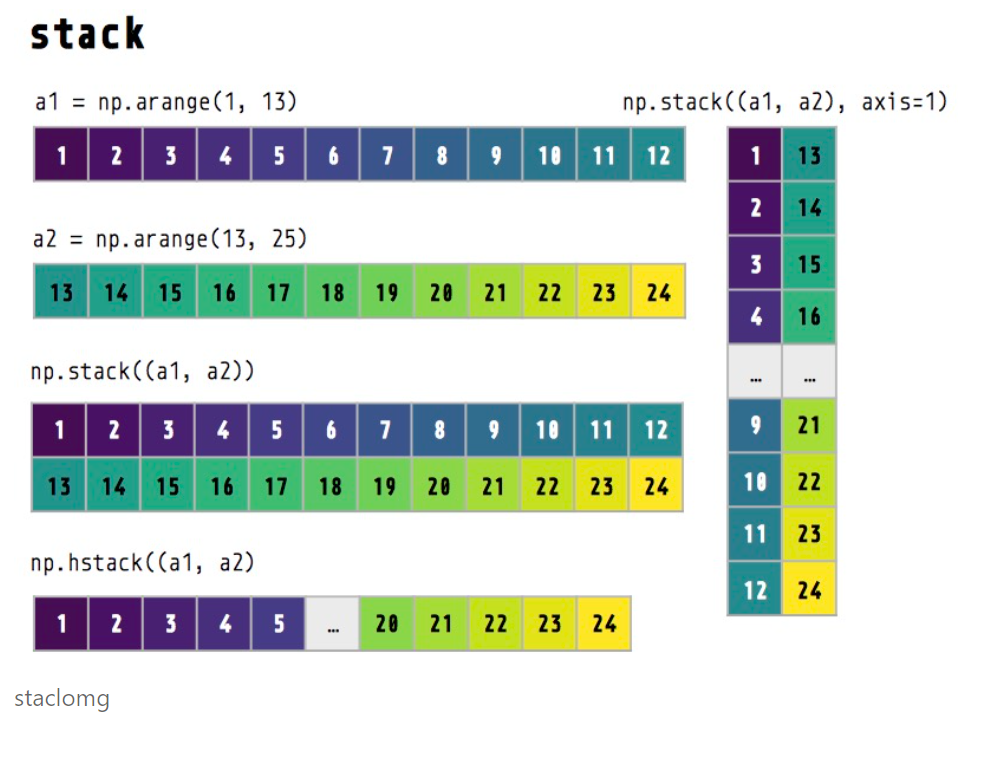
np.stack
# 一维数组堆叠为二维数组
a1 = np.arange(1, 13)
print("a1数组：", a1)

a2 = np.arange(13, 25)
print("a2数组：", a2)

stack0 = np.stack((a1, a1, a2, a2))     # 默认情况下 axis=0
print("a1和a2默认情况下(axis=0)堆叠：", stack0)

stack1 = np.stack((a1, a1, a2, a2), axis=1)
print("a1和a2垂直方向下(axis=0)堆叠：",stack1)

stack_long = np.hstack((a1, a2))
print(stack_long)

# 二维矩阵堆叠为三维

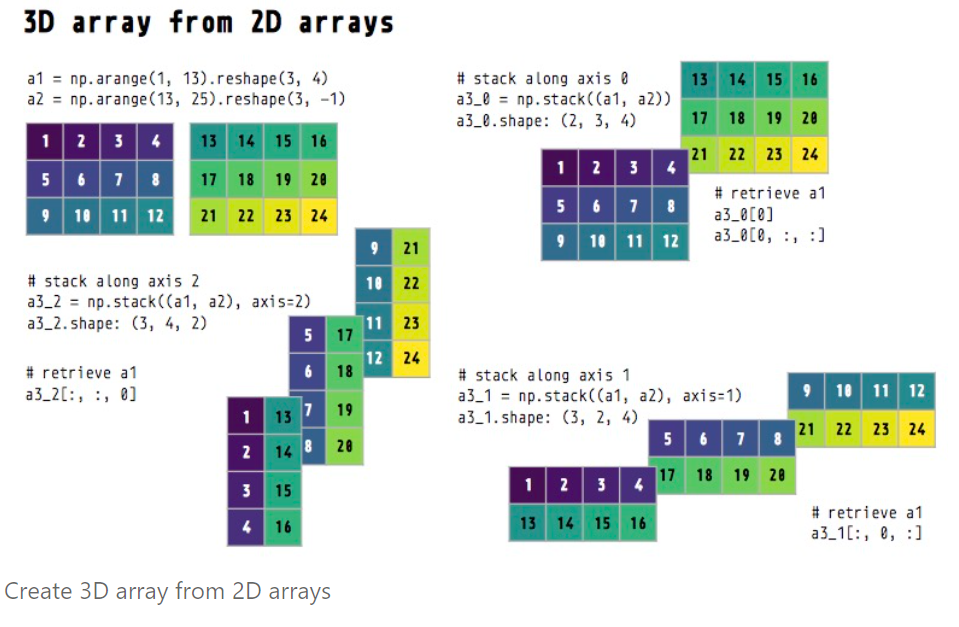
# 创建一个3*4的矩阵
a1_ = np.arange(1, 13).reshape(3, -1)  # 3_4
print("a1矩阵：", a1_)

# 创建另外一个3*4的矩阵
a2_ = np.arange(13, 25).reshape(3, -1)  # 3_4
print("a2矩阵：", a2_)

# a1和a2矩阵在默认axis=0方向上的堆叠
a3_0 = np.stack((a1_, a2_))             # default axis=0 (dimension 0)
print("堆叠a3_0矩阵的维度：", a3_0.ndim) 
print("堆叠a3_0矩阵的元素个数：", a3_0.size)  
print("堆叠a3_0矩阵的形状：", a3_0.shape)  # 2_3_4
print("堆叠a3_0矩阵的内容：", a3_0)

# a1和a2矩阵在默认axis=1方向上的堆叠
a3_1 = np.stack((a1, a2), axis=1)
print("堆叠a3_1矩阵的形状：", a3_1.shape)  # 3_2_4
print(a3_1)

# a1和a2矩阵在默认axis=2方向上的堆叠
a3_2 = np.stack((a1, a2), axis=2)  # dimension 2
print("堆叠a3_2矩阵的形状：",a3_2.shape)  # 3_4_2
print(a3_2)

科学计算神器之二Pytorch的使用

PyTorch也是一个常用的科学计算库，相比Numpy只能运行在CPU，PyTorch可以运行在GPU上，加快相关计算。

安装Pytorch

第一步：更换pypi的源，提升安装速度。

# 升级pip
python -m pip install --upgrade pip
# 更换 pypi 源加速库的安装
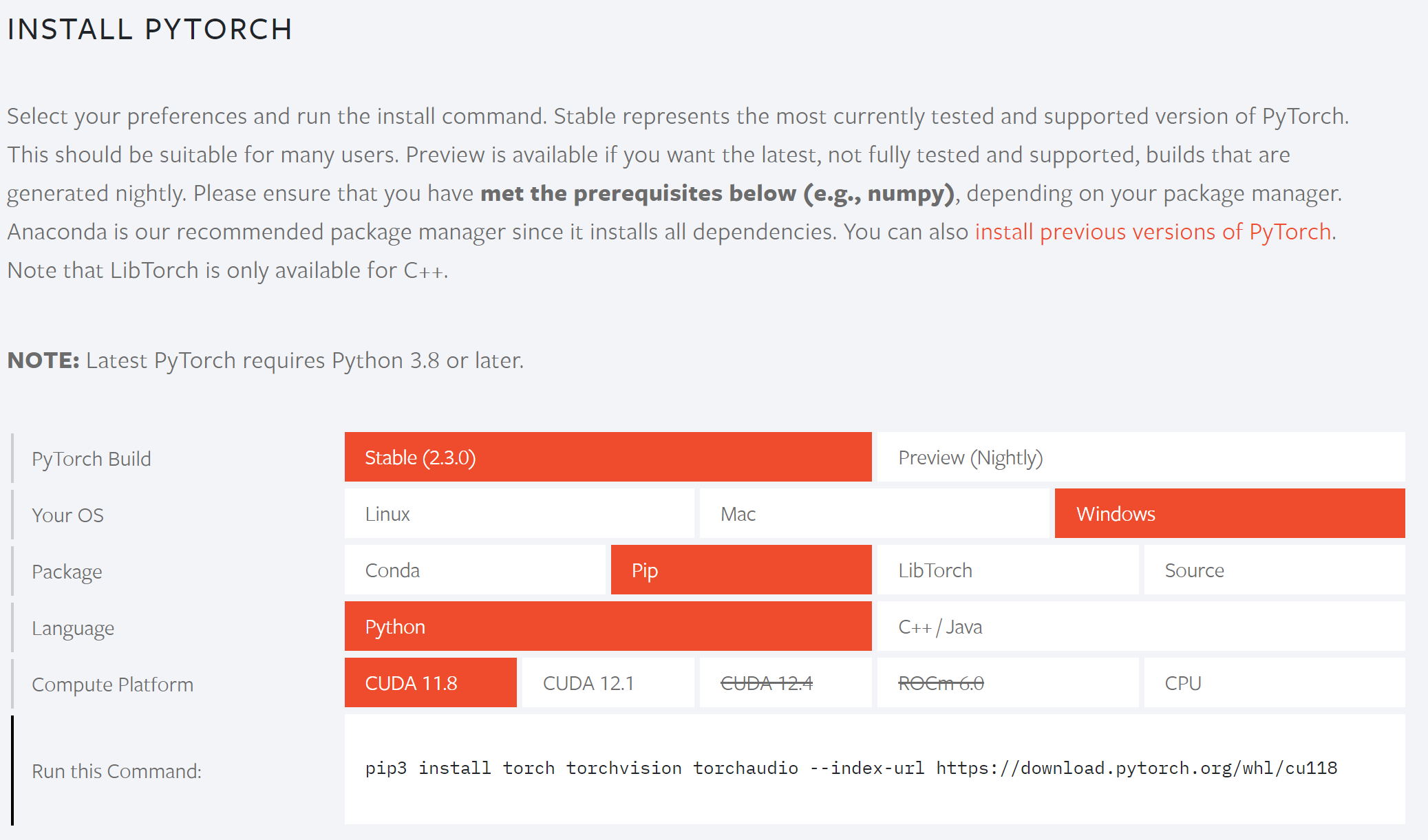
pip config set global.index-url https://pypi.tuna.tsinghua.edu.cn/simple

第二步：访问https://pytorch.org/ ,根据自己机器的环境选择对应的pytorch安装命令

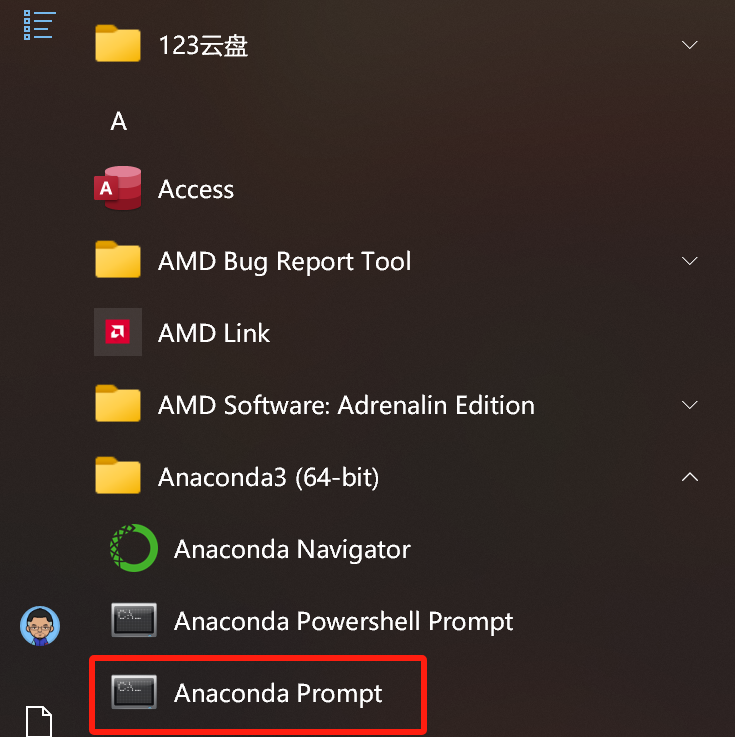
第三步：启动命令行，运行对应的安装命令

注意：如果使用的是jupyter，建议通过开始菜单启动anaconda prompt的方式运行命令行

# 如果操作系统=window、显卡有英伟达显卡、显存>4G，则可以运行如下命令：
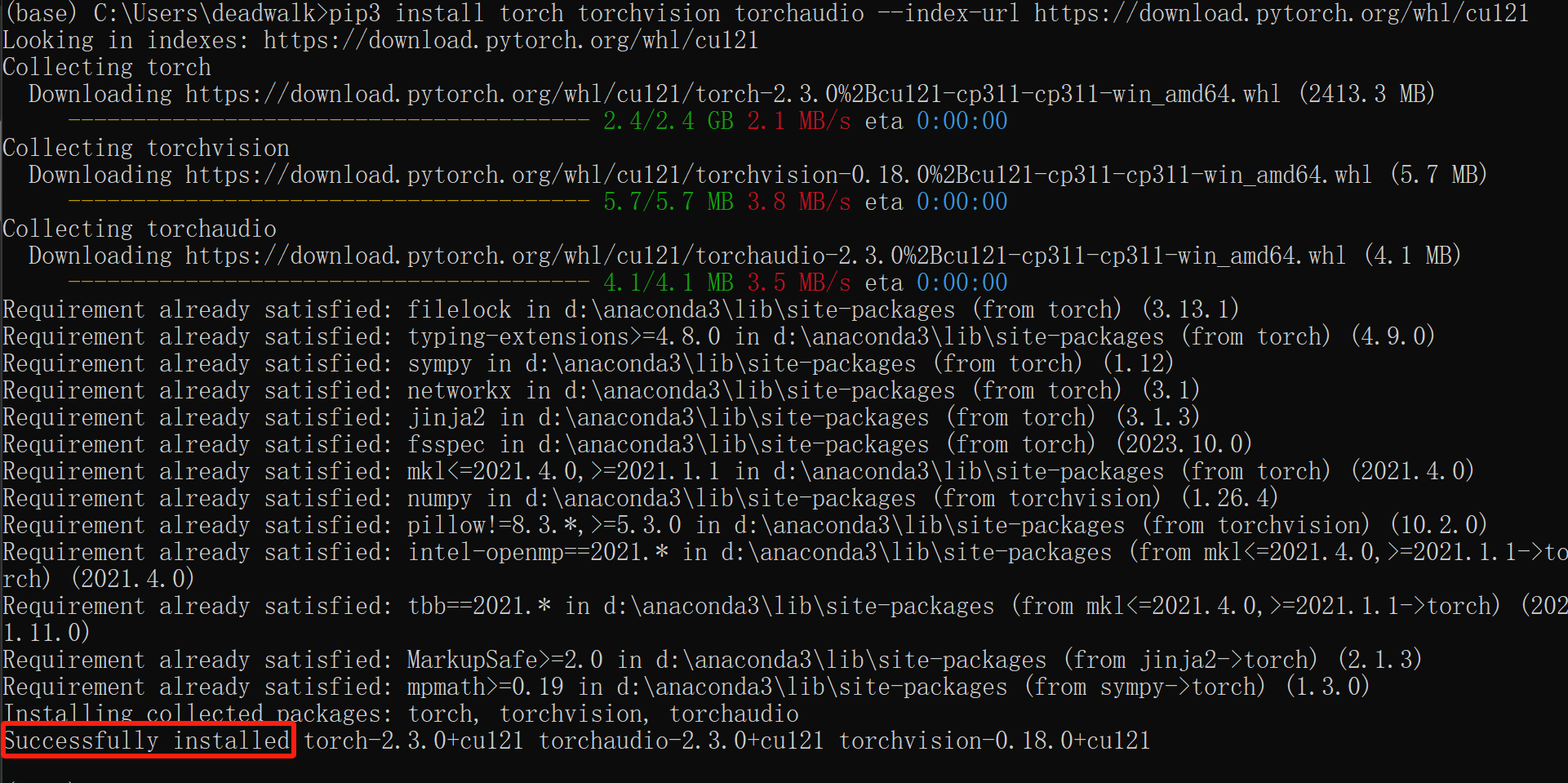
pip3 install torch torchvision torchaudio --index-url https://download.pytorch.org/whl/cu121
# 如果操作系统=window、无英伟达显卡、显存不够只能使用CPU，则可以运行如下安装命令：
pip3 install torch torchvision torchaudio
# 如果操作系统=Mac，则可以运行如下安装命令：
pip3 install torch torchvision torchaudio
# 如果操作系统=Linux，则可以运行如下安装命令：
pip3 install torch torchvision torchaudio

显示如下提示即成功安装

如果没有GPU环境或者安装pytorch一直不成功的话，也可以考虑租用云端GPU服务器。具体方法请见→《AutoDL平台的使用指南》

矩阵的基本操作(使用torch)

import torch

# 快速构建矩阵
matrix = torch.tensor([[1, 2, 3], [4, 5, 6]])

print("矩阵数据：", matrix)

# 查看矩阵的维度信息
print("矩阵维度：", matrix.dim())

# 查看矩阵的形状
print("矩阵形状：", matrix.size())

# 查看矩阵的size
print("矩阵size：", matrix.numel())

# 对矩阵进行reshape为一个矩阵
reshaped_matrix = matrix.view(3, 2)
print("重塑后的矩阵：\n", reshaped_matrix)

# 修改矩阵中的数据内容
matrix[0, 1] = 10
print("修改后的矩阵：\n", matrix)

# 将矩阵的数据类型转换
matrix = matrix.type(torch.float)
print("转换数据类型后的矩阵：\n", matrix)

# 随机生成一个新的矩阵
new_matrix = torch.rand(2, 3)
print("随机生成的新矩阵：\n", new_matrix)

矩阵的生成(使用torch)

import torch

# 生成一个形状为 (3, 4, 5) 的数组,内容都为0
tensor_zeros = torch.zeros((3, 4, 5))
print(tensor_zeros)

# 生成一个形状为 (3, 4, 5) 的数组,内容都为1
tensor_ones = torch.ones((3, 4, 5))
print(tensor_ones)

# 生成一个形状为 (3, 4, 5) 的数组，内容为随机
tensor_random = torch.rand(3, 4, 5)
print(tensor_random)

矩阵的堆叠和拼接(使用torch)

import torch

a = torch.arange(1, 28).reshape(3, 3, 3)
b = torch.arange(28, 55).reshape(3, 3, 3)

#  torch.cat((a, b), dim=2) 与 torch.stack((a, b), dim=2) 效果一样
print("torch.stack((a, b), dim=2)：", torch.stack((a, b), dim=2))
print("torch.cat((a, b), dim=2)：", torch.cat((a, b), dim=2))

#  torch.cat((a, b), dim=1) 与 torch.stack((a, b), dim=1) 效果一样
print("torch.stack((a, b), dim=1)：", torch.stack((a, b), dim=1))
print("torch.cat((a, b), dim=1)：", torch.cat((a, b), dim=1))

#  torch.cat((a, b), dim=0) 与 torch.stack((a, b), dim=0) 效果一样
print("torch.stack((a, b), dim=0)：", torch.stack((a, b), dim=0))
print("torch.cat((a, b), dim=0)：", torch.cat((a, b), dim=0))

通过以上对比可以发现

  • numpy和torch的使用方法基本一致，numpy支持的计算方法torch也支持。

  • 两者都提供了类似的数组/(torch里叫张量)操作，如索引、切片、广播、数学运算等。

  • numpy也可以与torch进行互转，例如：

    import numpy as np
import torch

# 创建一个 NumPy 数组
numpy_array = np.array([[1, 2, 3], [4, 5, 6]])

# 将 NumPy 数组转换为 PyTorch 张量
torch_tensor = torch.from_numpy(numpy_array)

# 创建一个 PyTorch 张量
torch_tensor = torch.tensor([[1, 2, 3], [4, 5, 6]])

# 将 PyTorch 张量转换为 NumPy 数组
numpy_array = torch_tensor.numpy()

print("NumPy 数组：\n", numpy_array)
print("PyTorch 张量：\n", torch_tensor)

数据信息

基本统计量

均值（Mean）

定义：均值是一组数据中所有数据值的总和除以数据值的个数。
作用：表示一组数据的平均值。

计算方法：均值 \mu = \frac{\sum_{i=1}^{n} x_i}{n}，其中 x_i 是数据集中的每个数据值，n 是数据值的个数。

标准差（Standard Deviation）

定义：标准差是方差的平方根，用于衡量数据值的离散程度。
作用：表示数据的离散程度。

计算方法：标准差 \sigma = \sqrt{\frac{\sum_{i=1}^{n} (x_i - \mu)^2}{n}}，其中 x_i 是数据集中的每个数据值，\mu 是均值，n 是数据值的个数。

方差（Variance）

定义：方差是每个数据值与均值之差的平方的平均值。
作用：表示数据与均值之间的差异程度。（如果比较离散的话，方差越大；如果比较集中的话，方差越小）

计算方法：方差 \sigma^2 = \frac{\sum_{i=1}^{n} (x_i - \mu)^2}{n}，其中 x_i 是数据集中的每个数据值，\mu 是均值，n 是数据值的个数。

示例代码：

import numpy as np

# 示例数据集
data = np.array([1, 2, 3, 4, 5])

# 计算均值
mean = np.mean(data)
# 计算标准差
std = np.std(data)
# 计算方差
variance = np.var(data)

print("均值:", mean)
print("标准差:", std)
print("方差:", variance)

file

数据预处理

归一化（Normalization）/ 线性映射：
  • 处理方式：将数据缩放到一个特定的范围，通常是[0, 1]或[-1, 1]。
  • 使用场景：在使用基于距离的算法（如KNN、SVM）时，需要对特征进行归一化，以避免某些特征对距离计算的影响过大。例如，在人脸识别中，对图像特征进行归一化可以确保不同特征之间的权重相对平衡，提高识别准确性。

备注：这里的归一化容易与上篇课程皮尔逊系数：协方差的归一化搞混，仔细查看皮尔逊系数是将两列数据变化趋势归一化到[-1,1]之间；此处的归一化是将一组数据归一化到[-1,1]之间。

import numpy as np

# 创建示例数据
data = np.array([1, 2, 3, 4, 5])

# 数据归一化
normalized_data = (data - np.min(data)) / (np.max(data) - np.min(data))

print("归一化后的数据：", normalized_data)
去中心化（Mean Normalization）/ 去均值 / center data：
  • 处理方式：计算数据集的均值，通过减去均值来实现，主要用于观察数据中哪些数据"做了贡献(正数)"，哪些数据"拖后腿"(负数)。
  • 使用场景：在处理时间序列数据时，去中心化可以消除数据的趋势和季节性变化，使模型更容易捕捉数据的周期性。例如，在股票市场分析中，去中心化可以帮助识别股票价格的短期波动。
import numpy as np

# 创建示例数据
data = np.array([1, 2, 3, 4, 5])

# 计算数据的平均值
mean = np.mean(data)

# 去中心化
zero_centered_data = data - mean

print("去中心化后的数据：", zero_centered_data)
规范化（Standardization）/ 规范化：
  • 处理方式：将数据转换为均值为0，标准差为1的分布，主要用于一眼看出哪些数据是噪声(也叫离群点)
  • 使用场景：在使用需要标准正态分布数据的模型（如线性回归、逻辑回归）时，可以使用规范化。例如，在文本分类中，对文本特征进行规范化可以提高分类器的准确性和稳定性。
import numpy as np

# 创建示例数据
data = np.array([1, 2, 3, 4, 5])

# 计算数据的平均值和标准差
mean = np.mean(data)
std = np.std(data)

# 规范化
standardized_data = (data - mean) / std

print("规范化后的数据：", standardized_data)

信息蕴含在数据的相对大小

信息往往蕴含在数据的相对大小中。

为了便于理解这句话，我们通过以下代码来直观了解。

from matplotlib import pyplot as plt
import numpy as np

# 生成随机分数数据
scores = np.random.randint(low=0, high=101, size=(50,))

# 中心化/去均值/center data
centered_scores = scores - scores.mean()

# 归一化（把所有的数据线性映射到[0, 1]）
normalized_scores = (scores - scores.min()) / (scores.max() - scores.min())

# 标准化/规范化减均值，除以标准差
standardized_scores = (scores - scores.mean()) / scores.std()

# 创建四个子图并绘制数据
fig, axs = plt.subplots(2, 2, figsize=(12, 8))

axs[0, 0].plot(scores)
axs[0, 0].set_title('Original Scores')

axs[0, 1].plot(centered_scores)
axs[0, 1].set_title('Centered Scores')

axs[1, 0].plot(normalized_scores)
axs[1, 0].set_title('Normalized Scores')

axs[1, 1].plot(standardized_scores)
axs[1, 1].set_title('Standardized Scores')

plt.tight_layout()
plt.show()

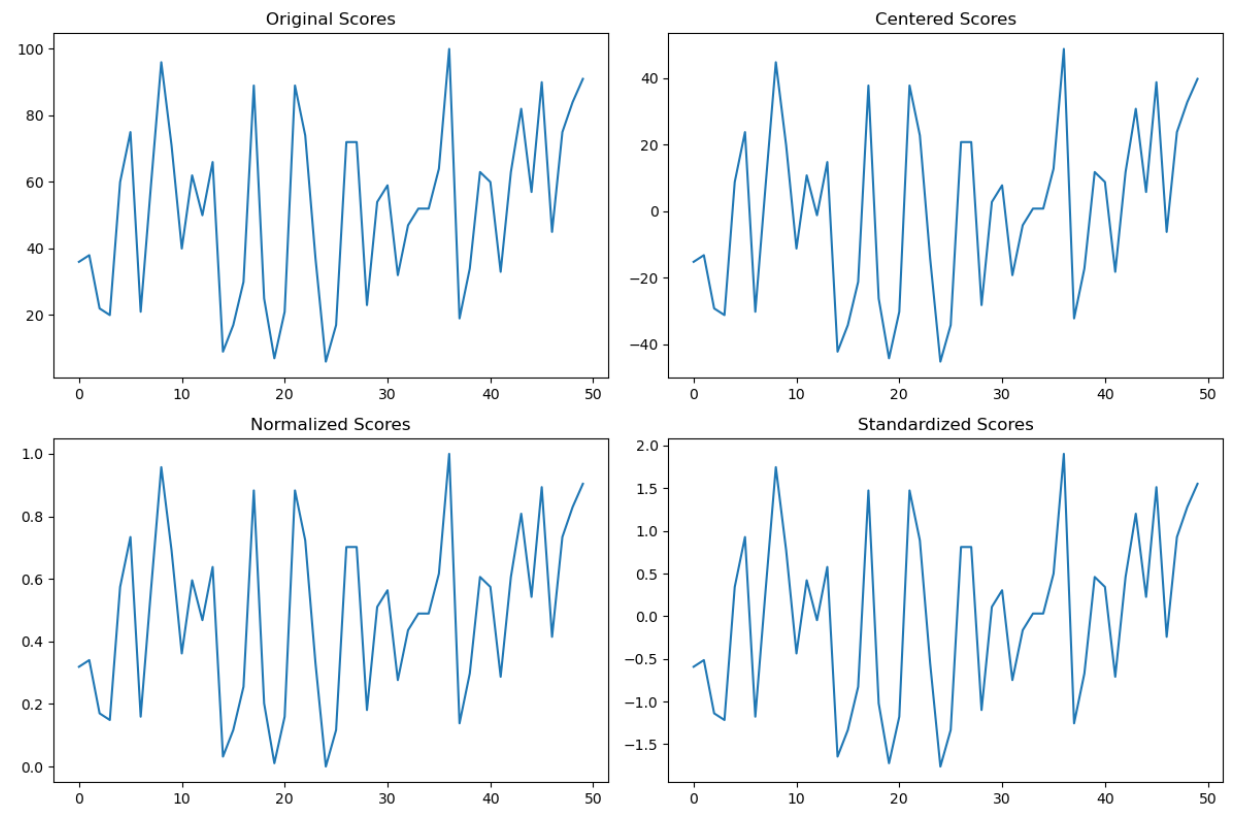
运行结果：

通过以上的对比可以看到，中心化Scores、归一化Scores、标准化Scores的数据虽然被修改了，与原始Scores不一样，但是数据中所表达的信息(曲线)仍然没有丢失，这即是信息蕴含在数据的相对大小。

数据预处理的应用

在机器学习当中，我们往往要对数据进行预处理，以提升数据质量，使得不同特征具有相似的尺度，有助于模型的收敛和性能提升。以下仍然使用鸢尾花的示例，来实际验证下数据预处理是否会对准确率有影响。

数据预处理的原则

  1. 特征和标签都需要预处理。

    • 一般来说，只需要预处理特征即可

  2. 训练集和测试集需要做一模一样的预处理。

  3. 预处理需要的参数，从训练集中提取

    例如：减均值时，均值从训练集中获得。原因是：训练集代表客观世界。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import plot_tree
import matplotlib.pyplot as plt

# 加载开源库中的iris数据集
X,y = load_iris(return_X_y=True)

# 切分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, 
                                                    shuffle=True, 
                                                    random_state=0) 

# 原始数据预测
from sklearn.tree import DecisionTreeClassifier

# 1, 构建模型
dtc0 = DecisionTreeClassifier(criterion='gini')

# 2, 训练模型
dtc0.fit(X=X_train, y=y_train)

# 3, 评估模型

acc = (dtc0.predict(X=X_test) == y_test).mean()
acc
# 预处理方式一：减均值(中心化)
X_train1 = X_train - _mean
X_test1 = X_test - _mean

# 使用原始数据
from sklearn.tree import DecisionTreeClassifier

# 1, 构建模型
dtc1 = DecisionTreeClassifier(criterion='gini')

# 2, 训练模型
dtc1.fit(X=X_train1, y=y_train)

# 3, 评估模型

acc = (dtc1.predict(X=X_test1) == y_test).mean()
acc
# 预处理方式二：归一化
X_train2 = (X_train - _min) / (_max - _min)
X_test2 =(X_test - _min) / (_max - _min)

# 使用原始数据
from sklearn.tree import DecisionTreeClassifier

# 1, 构建模型
dtc2 = DecisionTreeClassifier(criterion='gini')

# 2, 训练模型
dtc2.fit(X=X_train2, y=y_train)

# 3, 评估模型

acc = (dtc2.predict(X=X_test2) == y_test).mean()
acc
# 预处理方式三：规范化
X_train3 = (X_train - _mean) / (_std + 1e-9)
X_test3 =(X_test - _mean) / (_std + 1e-9)

# 使用原始数据
from sklearn.tree import DecisionTreeClassifier

# 1, 构建模型
dtc3 = DecisionTreeClassifier(criterion='gini')

# 2, 训练模型
dtc3.fit(X=X_train3, y=y_train)

# 3, 评估模型

acc = (dtc3.predict(X=X_test3) == y_test).mean()
acc

依次执行以上代码，可以看到原始数据、归一化数据、去中心化数据、规范化数据在训练之后，预测结果都为1.0。

内容小结

  • 在数据科学计算时，有两大工具可以使用：Numpy和Pytorch
  • Numpy使用的是CPU进行计算，更适合传统的数值计算任务；PyTorch 可以使用GPU计算，更适合深度学习任务。
  • 信息蕴含在数据的相对大小中，即是对数据做了修改但没有改变相对大小，那么信息仍然存在。
  • 在机器学习当中，我们往往要对数据进行预处理，以提升数据质量，使得不同特征具有相似的尺度，有助于模型的收敛和性能提升。
  • 数据预处理的方式一般有归一化、去中心化、规范化。
    • 归一化：将数据缩放到一个特定的范围，通常是[0, 1]或[-1, 1]
    • 去中心化：计算数据集的均值，通过减去均值来实现，主要用于观察数据中哪些数据"做了贡献(正数)"，哪些数据"拖后腿"(负数)。
    • 规范化：将数据转换为均值为0，标准差为1的分布，主要用于一眼看出哪些数据是噪声(也叫离群点)

欢迎关注公众号以获得最新的文章和新闻

1人评论了“【课程总结】Day5（上）：科学计算神器Numpy、Pytorch和数据预处理”

发表评论

您的邮箱地址不会被公开。 必填项已用 * 标注

分类文章

personal_logo
Dongming
自由职业者

推荐活动

推荐文章

【操作攻略】GPU云环境的使用介绍
2024-11-14
1 week ago
【项目实战】通过LLaMaFactory+Qwen2-VL-2B微调一个多模态医疗大模型
2024-10-27
3 weeks ago
【课程总结】day19（中）：Transformer架构及注意力机制了解
2024-08-02
3 months ago
【重拾数学知识】矢量的点乘和叉乘
2024-10-18
1 month ago
【课程总结】Day11（上）：手势图像识别实战(LeNet模型)
2024-06-24
4 months ago
【课程总结】day34：多模态大模型之ViT模型、CLIP模型论文阅读理解
2024-10-14
1 month ago
【目录】AI知识学习路线图
2024-05-21
6 months ago
【课程总结】day33：文生图StableDiffusion模型初步了解以及部署体验
2024-10-13
1 month ago
【课程总结】day32(下)：Xinference部署向量化模型
2024-10-10
1 month ago
【课程总结】day31：多模态大模型初步了解
2024-09-30
1 month ago
菜单

文章目录

→ 内容目录
滚动至顶部