文章目录
Toggle前言
本章内容主要是学习了概率相关的知识,包括:概率、离散型概率计算方法、连续性概率计算方法、条件概率等数理统计知识,同时结合高斯贝叶斯算法,对鸢尾花进行模型预测。
概率与数理统计
概率
概率是描述随机现象发生可能性的数学工具,是用来量化不确定性的概念。概率和数理统计在人工智能中用于辅助建模,其建模思想广泛应用于机器学习中的不同模型,如:高斯贝叶斯。
概念
定义:概率(Probability)是描述随机事件发生可能性的数值,通常表示为介于 0 到 1 之间的实数。概率为 0 表示事件不可能发生,概率为 1 表示事件一定发生。
概率是一种固有属性,因为求概率是比较难的,所以我们往往使用频率(frequency,在实际观测或试验中,某一事件发生的次数与总试验次数之比)来代替。- 当实验次数越来越多时,频率就趋近于概率。在工程实践中,数据量很大时,概率直接拿频率来代替即可。
基本特性
-
非负性:概率值始终是非负的,即概率值不会为负数,即:1 >= P(A) >= 0
-
规范性:所有可能事件的概率之和等于1,即:P(A) + P(B) + P(B) … = 1
计算方法
离散型变量
概念
- 离散型变量是指有限的状态中选一个变量。
- 举例:
- 例如:交通灯有红灯、绿灯、黄灯;
- 例如:性别有男、女、未知;
离散量一般需要编码,编码的方式常见的有下面两种:
Zero index编码
- 编码是从0开始,例如:0, 1, 2, 3, 4,…, N-1
- 编码本身有大小,但是这个大小并没有数学内涵
例如:编码1和编码4,它们只是一个编码,它们是平等的,并不存在类似考试成绩的排名,这个就是值没有数学内涵。
One hot编码
- 编码是向量编码,其形式一般为:
0: [1, 0, 0, 0, 0, ... ] 1: [0, 1, 0, 0, 0, ... ] 2: [0, 0, 1, 0, 0, ... ]备注:one hot是一种重要的编码,它从一开始认为人人平等,这一思想在自然语言处理中是核心理念。
离散量计算概率的例子
- 假定有一个离散量做实验得到的数据为:[1, 2, 2, 2, 3, 1, 1]
- 计算方法:(出现个数/总的个数)
- 概率:
- 事件1出现的概率P(1) = 3 / 8
- 事件2出现的概率P(2) = 4 / 8
- 事件3出现的概率P(3) = 1 / 8
以鸢尾花为例,通过代码求得各个类别的出现概率,代码如下:
from sklearn.datasets import load_iris
# 加载开源库中的iris数据集
X,y = load_iris(return_X_y=True)
P_y0 = (y == 0).mean()
P_y1 = (y == 1).mean()
P_y2 = (y == 2).mean()
print(f'类别0的鸢尾花出现概率P(0) = ', P_y0)
print(f'类别1的鸢尾花出现概率P(1) = ', P_y1)
print(f'类别2的鸢尾花出现概率P(2) = ', P_y2)补充知识点:
以上计算得到的是先验概率,先验概率是指已经形成既定事实的概率分布,其是与生俱来的,改变不了的。
连续型变量
定义
-
连续型变量是指可以取无限个数值的变量,其取值可以在一个区间内任意取值。
例如:
[0, 1]:一个从 0 到 1 的连续量中间可以有无数个采样结果 -
严格意义上:
- 对于连续量的某个单点(例如:0.6),这个点的概率是0(因为宽度为0,求积分为0)
- 连续量的概率是
概率密度函数积分,单点的积分上下限是0
理论中的定义,在现实中是不太可能的,例如:在物理中经常提到在光滑的平面上求得….,完全光滑的平面在现实中是不存在的。所以,在工程中要进行化简,而人工智能是纯理论数学的工程化简。
概率密度函数
上述对连续量的概率介绍时,提到了一个重要的概念为概率密度函数(PDF, Probability Density Function)
- 概率密度函数是概率的导函数(概率密度函数→求积分→概率)
- 概率是概率密度函数的积分(概率→求微分→概率密度函数)
- 概率密度函数是比较常见的,其中便有:高斯分布
高斯分布(正态分布)
-
定义:高斯分布是一种连续型概率分布,其曲线呈钟形,对称分布在均值处,并由均值和方差两个参数完全描述。
-
高斯分布的概率密度函数为:
f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}其中,
\mu是均值,\sigma是标准差。 -
Python绘制高斯分布:
import numpy as np
from matplotlib import pyplot as plt
def gaussian(x, mu, sigma):
"""
计算高斯分布的概率密度函数值
参数:
x: 随机变量
mu: 均值
sigma: 标准差
返回:
高斯分布的概率密度函数值
"""
return 1/(np.sqrt(2*np.pi)*sigma) * np.exp(-(x - mu)**2 / (2*sigma**2))
# 测试高斯分布函数
x = np.linspace(start=-5, stop=5, num=100)
mu = 0
sigma = 1
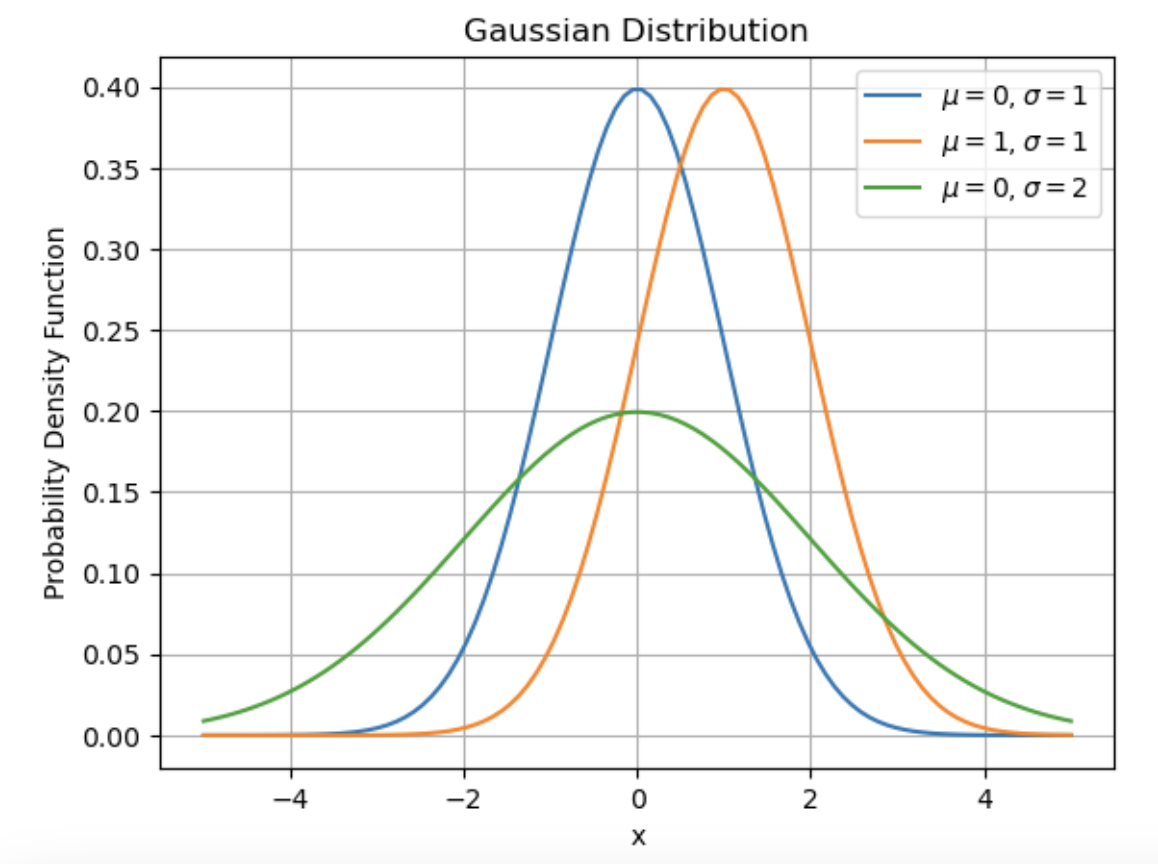
# 可视化高斯分布
plt.plot(x, gaussian(x, mu=0, sigma=1), label="$\mu=0, \sigma=1$")
plt.plot(x, gaussian(x, mu=1, sigma=1), label="$\mu=1, \sigma=1$")
plt.plot(x, gaussian(x, mu=0, sigma=2), label="$\mu=0, \sigma=2$")
plt.title('Gaussian Distribution')
plt.xlabel('x')
plt.ylabel('Probability Density Function')
plt.grid(True)
plt.legend()
plt.show()理论中的概率与工程中的概率
如果要求一个高斯分布函数上某一点的概率,其方法为求曲线的积分:
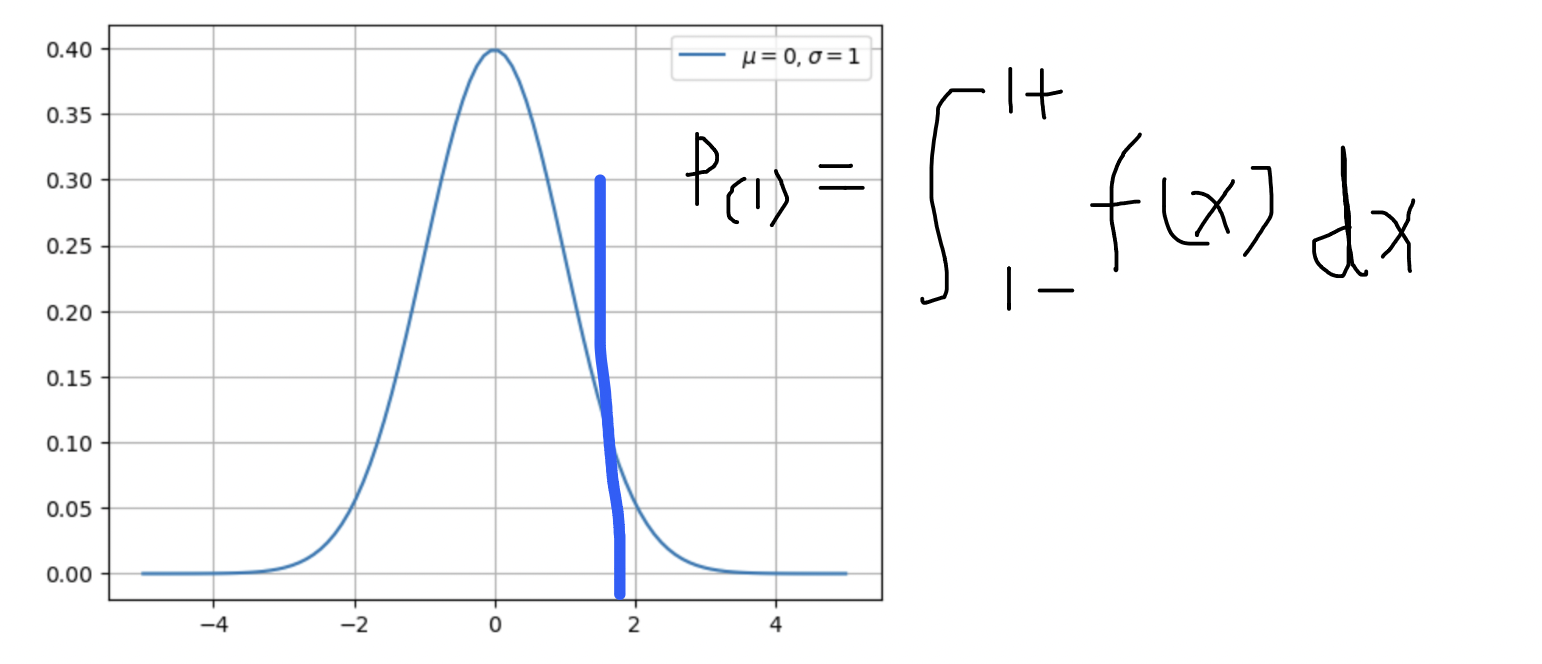
如果按照理论的方法是求不了概率的(因为理论中任意一点的宽度为0,进而概率也为0),所以我们需要进行工程化简。
核心思想:常规情况下,模型中对概率的使用,
- 重在比较概率的大小,而不是计算概率的具体数值是多少
- 求连续量的概率时,往往使用概率密度函数的值来代替概率的值(原因:求得是相对大小,而不是绝对大小)
连续量计算概率的例子
- 假定有一个连续量采样数据:[1, 2, 2, 2, 3, 1, 1]
- 计算方法:
- 计算概率密度函数来代替
- 由于上述采样数据的概率密度函数不可知,所以进一步工程化简
- 由于自然界普遍都是高斯分布,所以假定其是高斯分布即可
- 求概率的代码:
import numpy as np
def gaussian(x, mu, sigma):
"""
计算高斯分布的概率密度函数值
参数:
x: 随机变量
mu: 均值
sigma: 标准差
返回:
高斯分布的概率密度函数值
"""
return 1/(np.sqrt(2*np.pi)*sigma) * np.exp(-(x - mu)**2 / (2*sigma**2))
# 采样数据
logitis = np.array([1, 2, 2, 2, 2, 3, 1, 1])
# mu即为采样数据的均值
mu = logitis.mean()
# sigma即为采样数据的标准差
sigma = logitis.std()
# 求P(1)的概率
P1 = gaussian(x=1, mu=mu, sigma=sigma)
# 求P(2)的概率
P2 = gaussian(x=2, mu=mu, sigma=sigma)
# 求P(3)的概率
P3 = gaussian(x=3, mu=mu, sigma=sigma)
print(f'P(1)的概率为:',P1)
print(f'P(2)的概率为:',P2)
print(f'P(3)的概率为:',P3)条件概率
定义
条件概率是指在给定另一个事件发生的前提下,某一事件发生的概率。
表示方法
给定事件 B 发生的条件下,事件 A 发生的概率称为事件 A 在事件 B 条件下的条件概率,记作P(A|B)
一个例子
- 村里选村长,候选人有:
- 李:1, 2, 3;
- 王:1, 2;
- 刘:1
P(李1)当选的概率:
- 没有暗箱操作下,李1当选的概率是1/6;
- 如有暗箱操作(姓李的当选),李1当选概率低1/3。
以上问题是典型的条件概率。样本重组:上例中,已知姓李的当选时,进行了重新划分样本空间。
应对策略
根据条件,重新划分样本空间,将不满足条件的干掉,然后再计算概率。
公式推导
P(A|B) = P(AB) / P(B)
P(B|A) = P(AB) / P(A)
P(A|B) * P(B)= P(AB)
P(B|A) * P(A)= P(AB)
P(A|B) = P(B|A) * P(A) / P(B)
以上推导结果即为P(A|B)为B的条件下A发生的概率计算方法
P(y|X) = P(X|y) P(y) / P(X)
P(y0|X) = P(X|y0) P(y0) / P(X)
- X:一个输入样本的特征,包括[x1, x2, x3 …]
- y0:第0类
- 含义,在输入样本X的情况下,第0类的概率
P(y1|X) = P(X|y1) P(y1) / P(X)
P(y2|X) = P(X|y2) P(y2) / P(X)
在N分类问题上,通过计算输入样本条件下不同类别(y0,y1,y2..yn)的概率,然后选择概率最大的那个概率作为输出,这种方法即为贝叶斯算法,也叫高斯贝叶斯算法。
计算方法
P(y0|X) = P(X|y0) P(y0) / P(X)
P(y1|X) = P(X|y1) P(y1) / P(X)
P(y2|X) = P(X|y2) P(y2) / P(X)
P(y0|X) = P(X|y0) P(y0)
P(y1|X) = P(X|y1) P(y1)
P(y2|X) = P(X|y2) P(y2)
简化后的公式中:
- P(y0)、P(y1)、P(y2)的概率求解方法容易求得(因为是离散量,所以使用出现次数/总次数就可求得)。
- P(X|y0)的概率求解方法:
- 将类别为1和2的样本踢出去,然后求在类别0的情况下> X特征的概率。
- 由于X是一堆特征,所以P(X|y0)代表在类别0的条件> 下,x1、x2、x3这些独立特征同时发生的概率
P(y0|X) = P(x1,x2,x3..|y0) P(y0)
P(y1|X) = P(x1,x2,x3..|y1) P(y1)
P(y2|X) = P(x1,x2,x3..|y2) P(y2)
P(y0|X) = P(x1|y0)P(x2|y0)P(x3|y0)...P(xn|y0) P(y0)
P(y1|X) = P(x1|y1)P(x2|y1)P(x3|y1)...P(xn|y1) P(y1)
P(y2|X) = P(x1|y2)P(x2|y2)P(x3|y2) ...P(xn|y2)P(y2)
上述公式中,P(x1|y0)、P(x2|y0)…即可使用高斯模拟求得概率。
高斯贝叶斯只能进行分类,其虽然效果差一些(因为认为都属于高斯分布),但是计算速度非常快。
在计算机早期时代,在进行分类时使用的是高斯贝叶斯,当时还是非常重要的。
代码实现(使用sklearn)
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# 加载开源库中的iris数据集
X,y = load_iris(return_X_y=True)
# 切分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,
shuffle=True,
random_state=0)
# 引入高斯贝叶斯模型
from sklearn.naive_bayes import GaussianNB
# 1,构建模型
gnb = GaussianNB()
# 2,训练模型
gnb.fit(X=X_train, y=y_train)
# 3, 预测,将结果保存到y_pred
y_pred = gnb.predict(X=X_test)
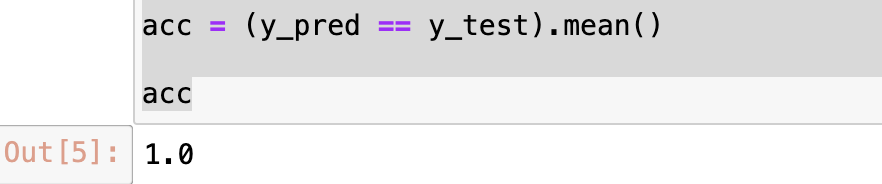
acc = (y_pred == y_test).mean()
acc代码实现(不使用sklearn)
import numpy as np
class MyGaussianNB(object):
def fit(self, X, y):
self.X = X
self.y = y
#根据训练数据集 y 中的类别标签,找出所有不重复的类别,并将其存储在 self.classes
self.classes = np.unique(y)
self.parameters = []
# 计算每个类别的均值和标准差
# 对 y 中类别进行遍历,将索引和对应的元素值分别赋给变量 i 和 c
for i, c in enumerate(self.classes):
# 取对应 y 类别中的 X
X_c = X[y == c]
self.parameters.append([])
# 遍历 X 的每一列数据,将计算的均值和标准差保存到parameters中
for col in X_c.T:
parameters = {"mean": col.mean(), "std": col.std()}
self.parameters[i].append(parameters)
def _calculate_likelihood(self, mean, std, x):
# 计算高斯分布的概率密度函数值
return (1 / (np.sqrt(2 * np.pi) * std)) * np.exp(-((x - mean) ** 2 / (2 * std ** 2)))
def _calculate_prior(self, c):
# 计算先验概率
return np.mean(self.y == c)
def predict(self, X):
preds = []
# 遍历 X 元素
for x in X:
posteriors = []
# 依次遍历 y 类别
for i, c in enumerate(self.classes):
likelihood = 1
# 使用之前已经计算好的均值和方差,代入到高斯密度函数中计算概率值
for j, param in enumerate(self.parameters[i]):
likelihood *= self._calculate_likelihood(param["mean"], param["std"], x[j])
# 计算P(y0)、P(y1)、P(y2)等先验概率
prior = self._calculate_prior(c)
# 计算P(x1|y0)P(x2|y0)P(x3|y0)...P(xn|y0) P(y0)的乘积
posterior = prior * likelihood
# 计算结果添加到posteriors列表中,用于后续求最大值
posteriors.append(posterior)
# 根据posteriors中的最大值的索引,在类别列表 self.classes 中找到对应的类别,
# 并将其添加到预测结果列表 preds 中
preds.append(self.classes[np.argmax(posteriors)])
return preds
调用模型
# 1,构建模型
mygnb = MyGaussianNB()
# 2,训练模型
mygnb.fit(X=X_train, y=y_train)
# 3, 预测,将结果保存到y_pred
y_pred = mygnb.predict(X=X_test)
acc = (y_pred == y_test).mean()
acc
计算结果也为1.0,myGaussianNB与sklearn的GaussianNB计算结果一致。
基本统计量
均值(Mean)
定义:均值是一组数据中所有数据值的总和除以数据值的个数。
作用:表示一组数据的平均值。
计算方法:均值 \mu = \frac{\sum_{i=1}^{n} x_i}{n},其中 x_i 是数据集中的每个数据值,n 是数据值的个数。
标准差(Standard Deviation)
定义:标准差是方差的平方根,用于衡量数据值的离散程度。
作用:表示数据的离散程度。
计算方法:标准差 \sigma = \sqrt{\frac{\sum_{i=1}^{n} (x_i - \mu)^2}{n}},其中 x_i 是数据集中的每个数据值,\mu 是均值,n 是数据值的个数。
- 1,求均值
- 2,求每个数跟均值的差
- 3,把差取平方
- 4,再把平方的结果取均值
- 5,再把结果取平方根
方差(Variance)
定义:方差是每个数据值与均值之差的平方的平均值。
作用:表示数据与均值之间的差异程度。(如果比较离散的话,方差越大;如果比较集中的话,方差越小)
计算方法:方差 \sigma^2 = \frac{\sum_{i=1}^{n} (x_i - \mu)^2}{n},其中 x_i 是数据集中的每个数据值,\mu 是均值,n 是数据值的个数。
示例代码:
import numpy as np
# 示例数据集
data = np.array([1, 2, 3, 4, 5])
# 计算均值
mean = np.mean(data)
# 计算标准差
std = np.std(data)
# 计算方差
variance = np.var(data)
print("均值:", mean)
print("标准差:", std)
print("方差:", variance)协方差(Covariance)
定义:协方差衡量两个变量一起变化的程度。
作用:考察两列数据的变化趋势是否相同
计算方法:协方差 \text{Cov}(X, Y) = \frac{\sum_{i=1}^{n} (X_i - \mu_X)(Y_i - \mu_Y)}{n},其中 X_i 和 Y_i 分别是两个变量中的每个数据值,\mu_X 和 \mu_Y 分别是两个变量的均值,n 是数据值的个数。
皮尔逊相关函数
- 把协方差归一化
- 范围[-1, 1]
- -1:严格负相关
- 1:严格正相关
- 0:不相关
X = np.array([1, 3, 5, 7, 9])
Y = np.array([2, 4, 6, 8, 10])
Z = Y[::-1]
covariance_x_y = ((X - X.mean()) * (Y - Y.mean())).mean()
covariance_x_z = ((X - X.mean()) * (Z - Z.mean())).mean()
# 计算标准差
std_X = X.std()
std_Y = Y.std()
std_Z = Z.std()
# 计算皮尔逊相关系数
pearson_corr_x_y = covariance_x_y / (std_X * std_Y)
pearson_corr_x_z = covariance_x_z / (std_X * std_Z)
print("X和Y归一化结果为:", pearson_corr_x_y)
print("X和Z归一化结果为:", pearson_corr_x_z)内容小结
- 概率和数理统计是一种建模思想,其中使用较多的高斯贝叶斯算法就是这一思想的实践。
- 概率是一种固有属性,其有非负性和规范性两个特性
- 概率计算时分离散型变量和连续相变量两种
- 离散型变量概率计算使用出现次数/ 总的次数即可
- 连续型变量概率计算方法较为复杂,需要进行工程化简+假定为高斯分布来进行计算
- 常规情况下,由于我们重在比较概率大小,而不是计算具体数值,所以使用概率密度函数的值来代替概率的值
- 条件概率也是一种概率
- 条件概率的计算方法大致思想是将在X输入样本的情况下,计算对应类的概率,最后求得概率最大的作为输出。这一方法也叫高斯贝叶斯方法。
- 高斯贝叶斯只能进行分类,其效果虽然差一些(因为认为都属于高斯分布),但是计算速度非常快。在计算机早期发展时期,NLP等自然语言处理时常用高斯贝叶斯。
欢迎关注公众号以获得最新的文章和新闻

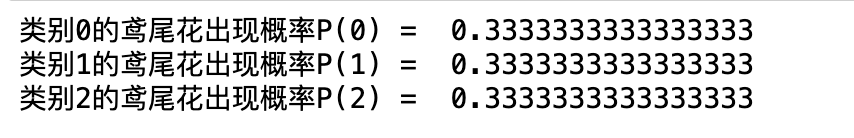







2人评论了“【课程总结】Day3:概率和贝叶斯算法”
1 / np.sqrt(2 * np.pi) / sigma * np.exp(-(x – mu) ** 2 / 2 / sigma ** 2 )
高斯分布的概率密度函数的code里面有个运算符写错了,应该是“/”,你写的是*
找chatGPT确认了一下:
return 1 / np.sqrt(2 * np.pi) / sigma * np.exp(-(x – mu) ** 2 / 2 / sigma ** 2 )
return 1 / (np.sqrt(2 * np.pi) * sigma) * np.exp(-(x – mu) ** 2 / ( 2 * sigma ** 2))
这两个表达式是等价的,因为它们仅仅是在除法运算的括号位置上有所不同。