前言
在机器学习中，距离度量在CV 、NLP以及数据分析等领域都有众多的应用。最常见的距离度量有余弦距离
相关概念
余弦相似度
余弦相似度又称为余弦相似性，是通过计算两个向量的夹角余弦值
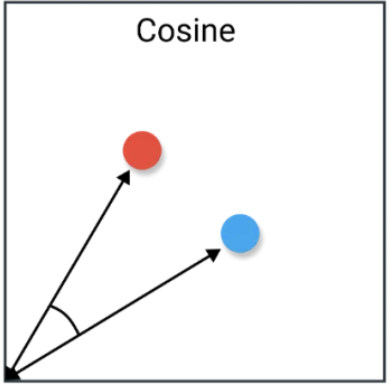
余弦相似度计算公式
\text{余弦相似度} = \frac{A \cdot B}{\|A\| \cdot \|B\|}其中，A · B 表示向量 A 和 B 的点积（内积），|A| 和 |B| 分别表示向量 A 和 B 的模长。
通过以上公式，可以看到其中涉及的数学知识有：
- 向量
- 向量的模长
- 向量的基本计算
- 向量的内积
- 向量的投影
- 余弦夹角
- 余弦定理
……
- 余弦定理
为了系统掌握上述内容，我们对以上数学知识进行重新梳理。
向量
向量的定义
向量是具有大小和方向的量，通常用箭头表示。在数学中，向量可以用来表示空间中的点、力、速度等概念。
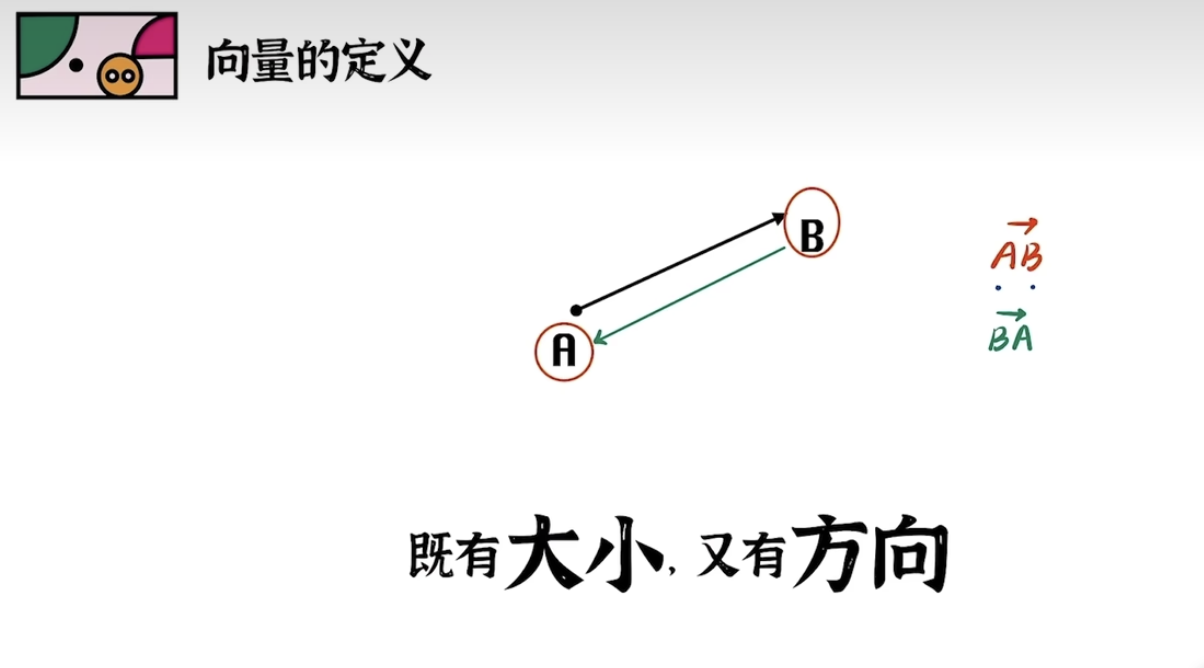
在数学和物理学中，"矢量"和"向量"这两个术语通常被用来表示相同的概念，即具有大小和方向的量。它们之间没有本质上的区别，可以互相替换使用。
在数学中，我们通常使用"向量"这个术语来表示这种量;
在物理学中，更常见的是使用"矢量"这个术语来描述这种性质。
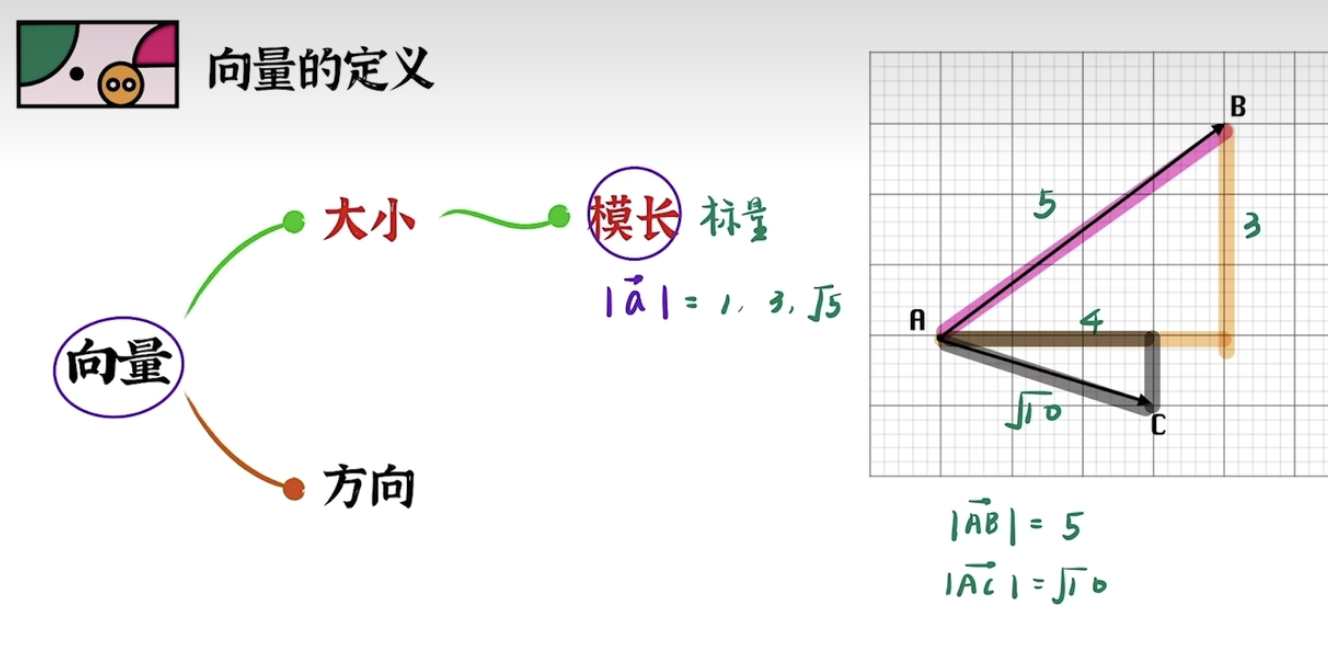
向量的大小
向量的大小通常称为模长
表示方法：一般是在向量表示符两侧增加竖线|A|
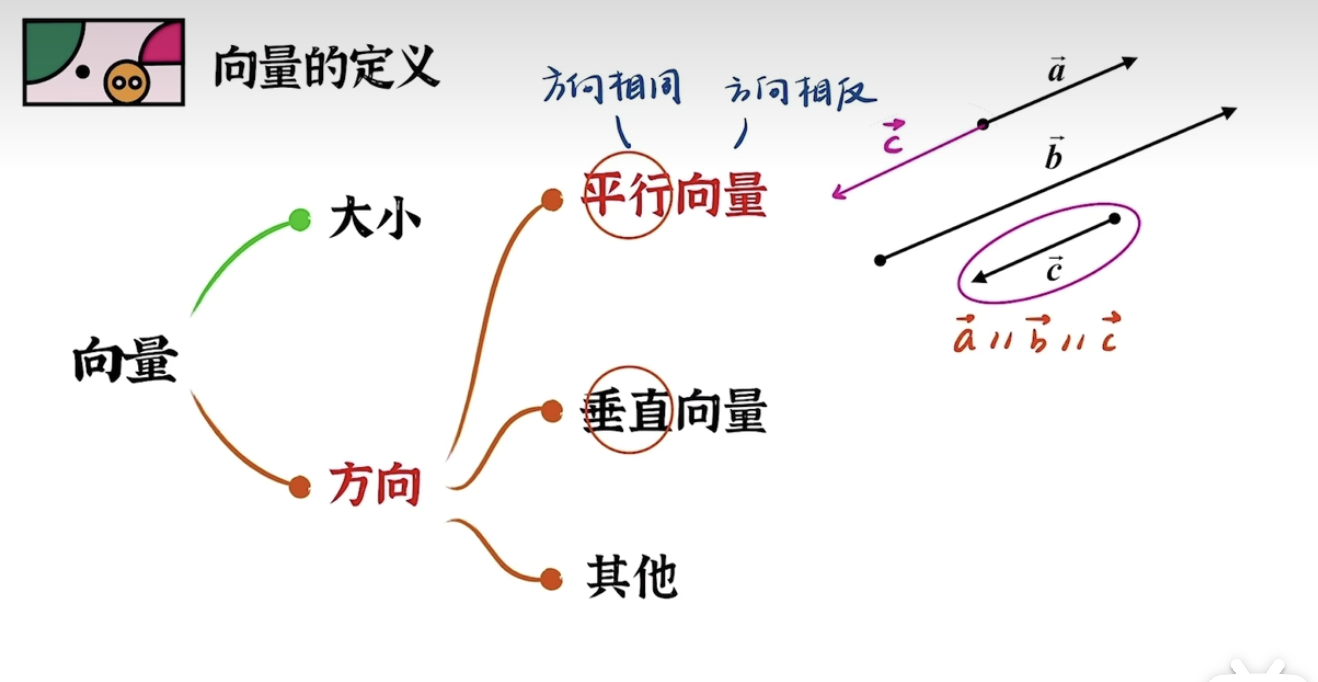
向量的方向
向量的方向是指向量所指的位置或指向。在二维空间中，方向通常用与 x 轴的夹角来表示。
两个向量常见的方向关系有：平行向量、垂直向量和其他。
向量的计算
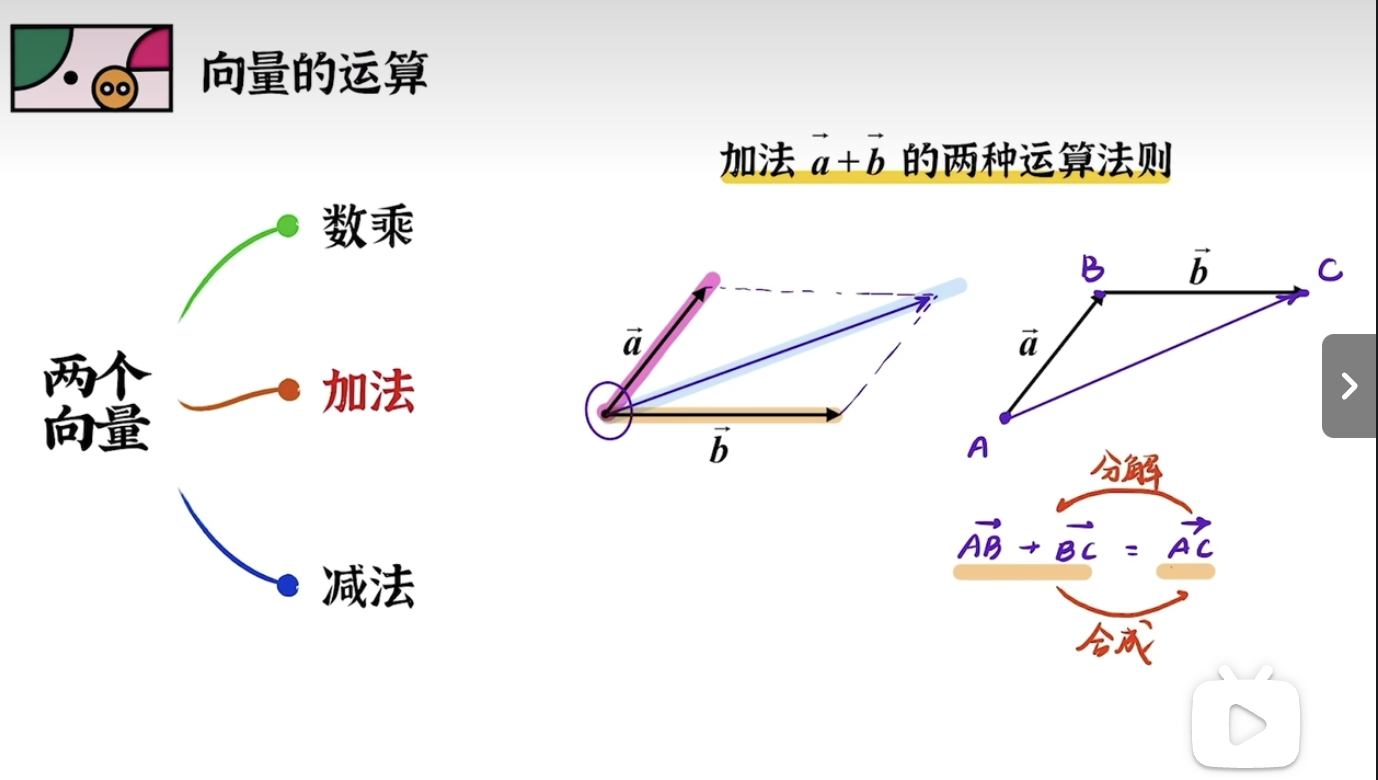
向量的加法
向量加法是将两个向量相加的操作。对于二维向量
\vec{a} = \vec{AB}和
\vec{b} = \vec{BC}它们的和为：
\vec{a} + \vec{b} = \vec{AB} + \vec{BC} = \vec{AC}
向量的减法
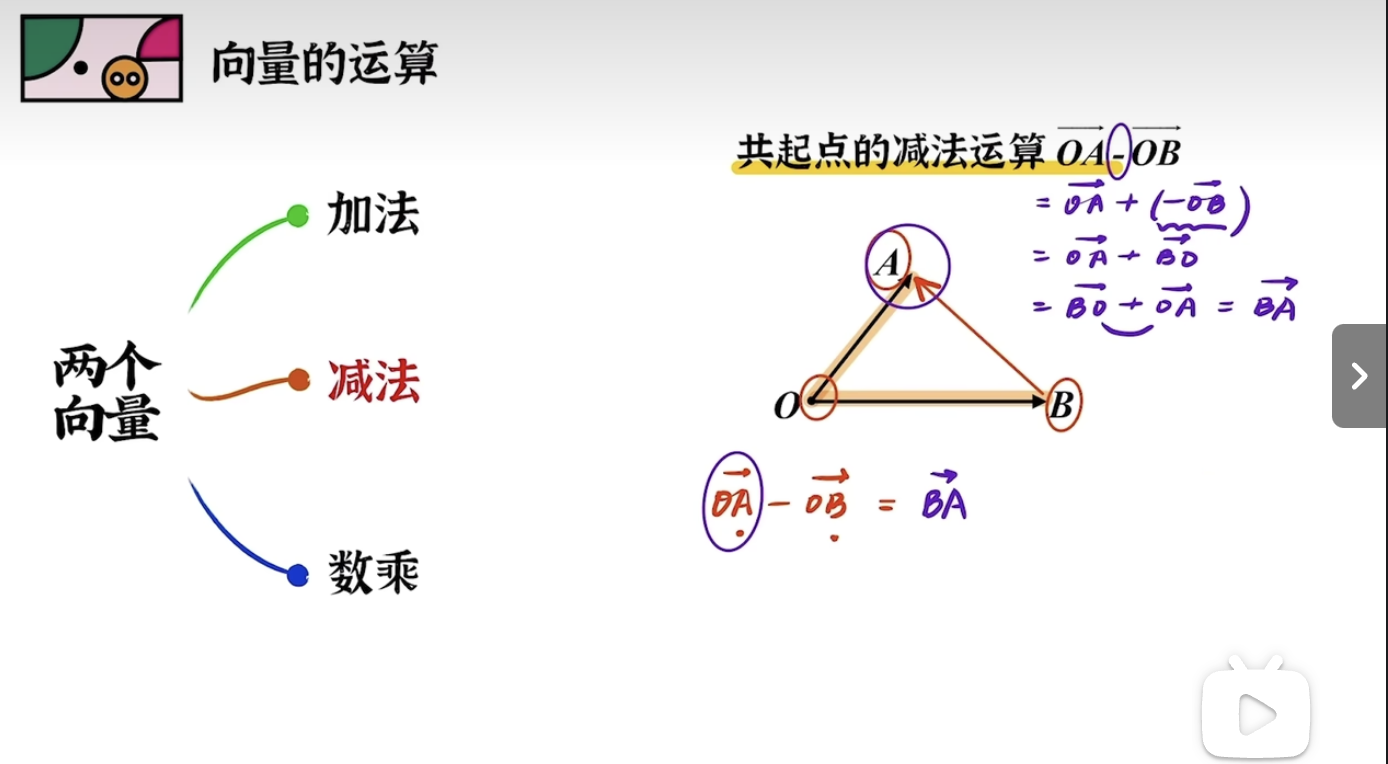
向量减法是将一个向量减去另一个向量的操作。对于二维向量
\vec{OA} = (a_1, a_2)和
\vec{OB} = (b_1, b_2)它们的差为：
\vec{OA} - \vec{OB} = \vec{OA} + (-\vec{OB}) = \vec{OA} + \vec{BO} = \vec{BO} + \vec{OA} = \vec{BA}
向量的数乘
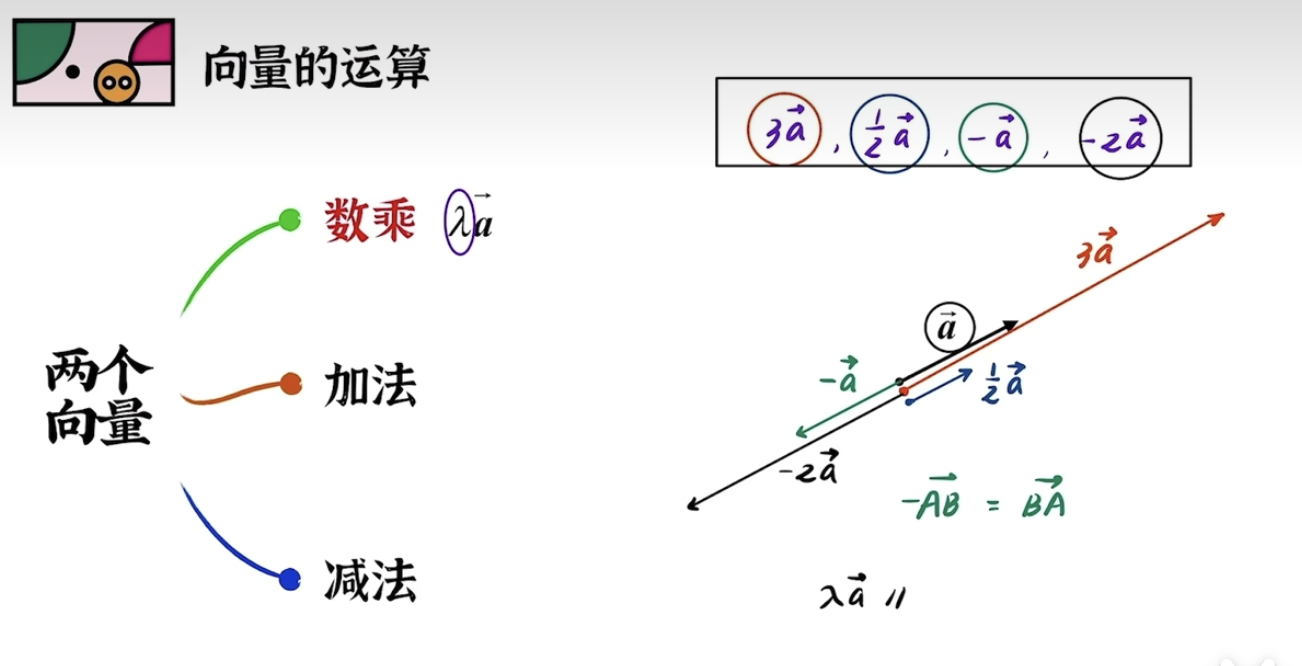
数量乘法是将一个标量与一个向量相乘的操作。标量乘以向量时，会使向量的大小增大或缩小，但方向不变。例如，标量lambda 与二维向量
\vec{A} = (a_1, a_2)的乘积为：
\lambda\vec{A} = (\lambda a_1, \lambda a_2)
向量的内积
点积是一种向量运算，也称为内积。对于二维向量
\vec{A} = (a_1, a_2)和
\vec{B} = (b_1, b_2)它们的点积为：
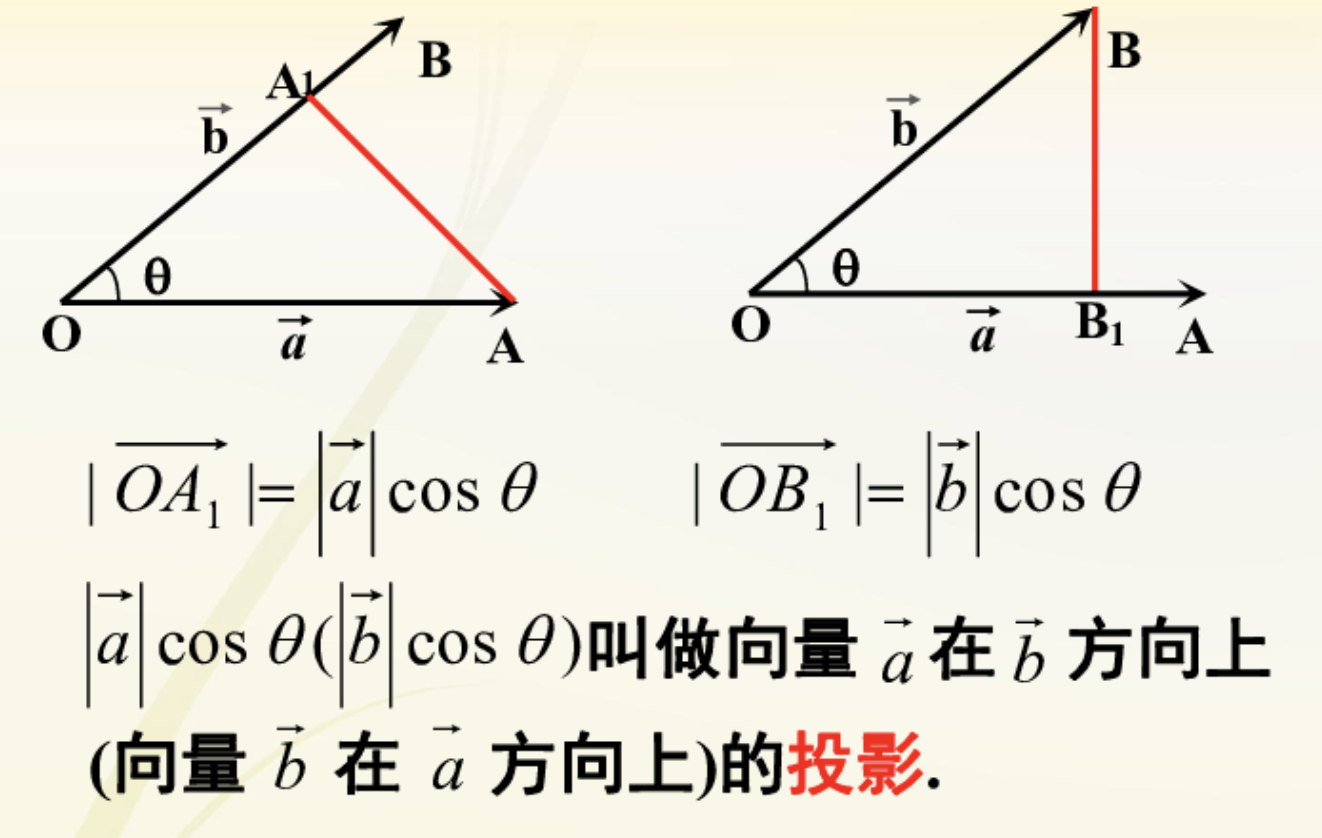
\vec{A} \cdot \vec{B} = a_1b_1 + a_2b_2
向量的投影
向量的投影是指一个向量在另一个向量上的投影，可以帮助我们理解向量之间的关系和计算向量之间的夹角。
正余弦定理
正弦定理
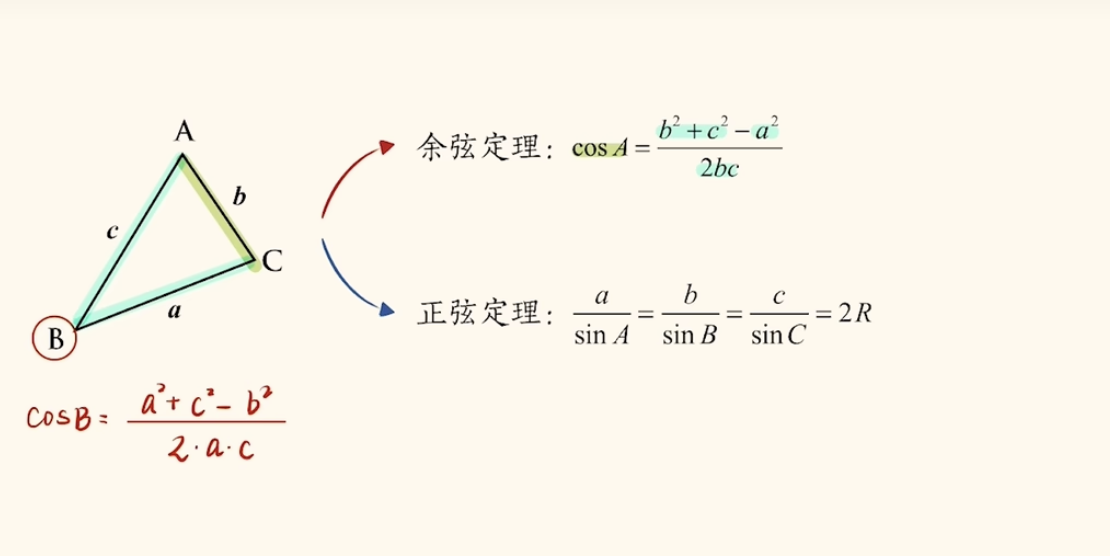
- 定义：正弦定理描述了三角形中角度和边长之间的关系。对于三角形 ABC，其三个顶点分别为 A、B、C，对应的边长分别为 a、b、c，以及对应的角度为 A、B、C，则正弦定理可以表示为：
\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} - 应用：可用于计算三角形中缺失的边长或角度，特别适用于非直角三角形。
余弦定理
- 定义：余弦定理描述了三角形中边长和角度之间的关系。对于三角形 ABC，其三个顶点分别为 A、B、C，对应的边长分别为 a、b、c，以及对应的角度为 A、B、C，则余弦定理可以表示为：
- a^2 = b^2 + c^2 - 2bc \cos A- b^2 = a^2 + c^2 - 2ac \cos B- c^2 = a^2 + b^2 - 2ab \cos C - 应用：可用于计算三角形中的边长或角度，特别适用于已知两边和夹角的情况。
