Search
内容目录

线性回归

分类与线性回归

假设有以下两种场景：

  • 场景一：假设你要开发一个垃圾邮件过滤器。通过收集大量的已标记为垃圾邮件和非垃圾邮件的电子邮件数据，利用分类算法训练模型，使其能够自动识别新收到的邮件是垃圾邮件还是正常邮件。

  • 场景二：假设你想预测房屋价格。通过收集房屋的特征（如面积、卧室数量、地理位置等）和相应的实际销售价格数据，利用线性回归模型建立特征与房屋价格之间的关系，从而预测未来房屋的价格。

对比以上两个场景：

  • 场景一旨在预测数据所属的类别，而场景二旨在预测连续数值输出。
  • 场景一输出离散的类别标签，而场景二输出连续的数值。

在机器学习中，分类(即：场景一)和线性回归(即：场景二)是两种常见的学习任务。

什么是线性回归

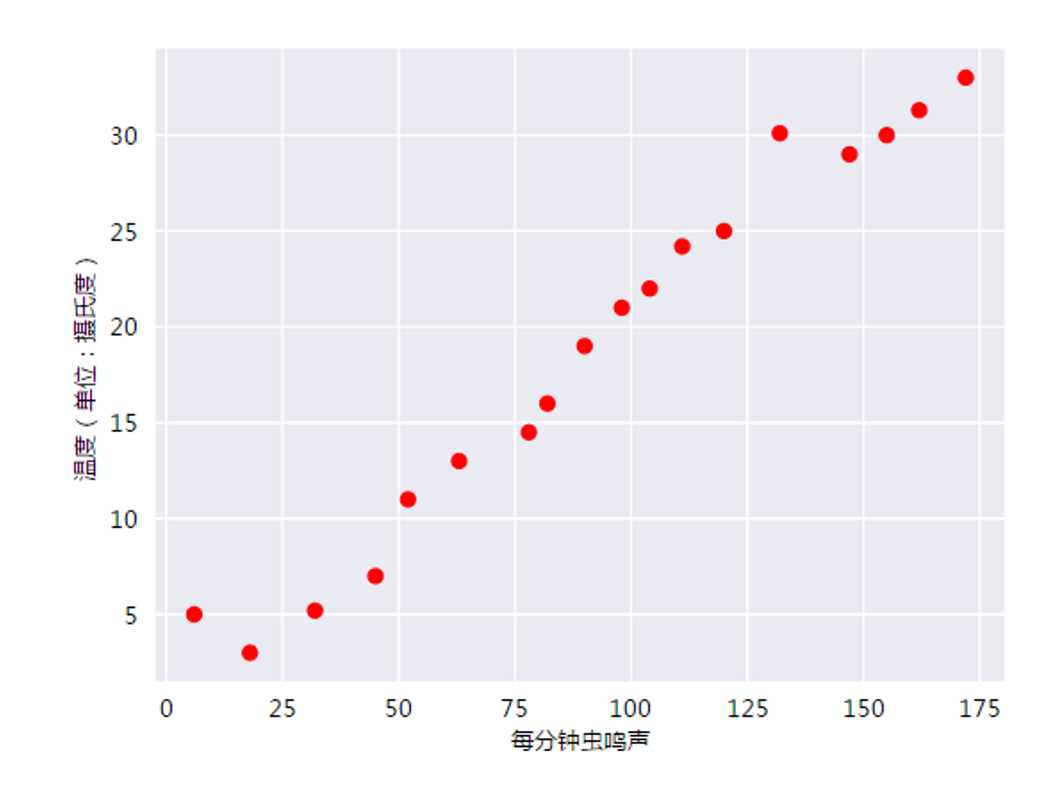
人们早就知晓，相比凉爽的天气，蟋蟀在较为炎热的天气里鸣叫更为频繁。数十年来，专业和业余昆虫学者已将每分钟的鸣叫声和温度方面的数据编入目录，通过将数据绘制为图表如下：

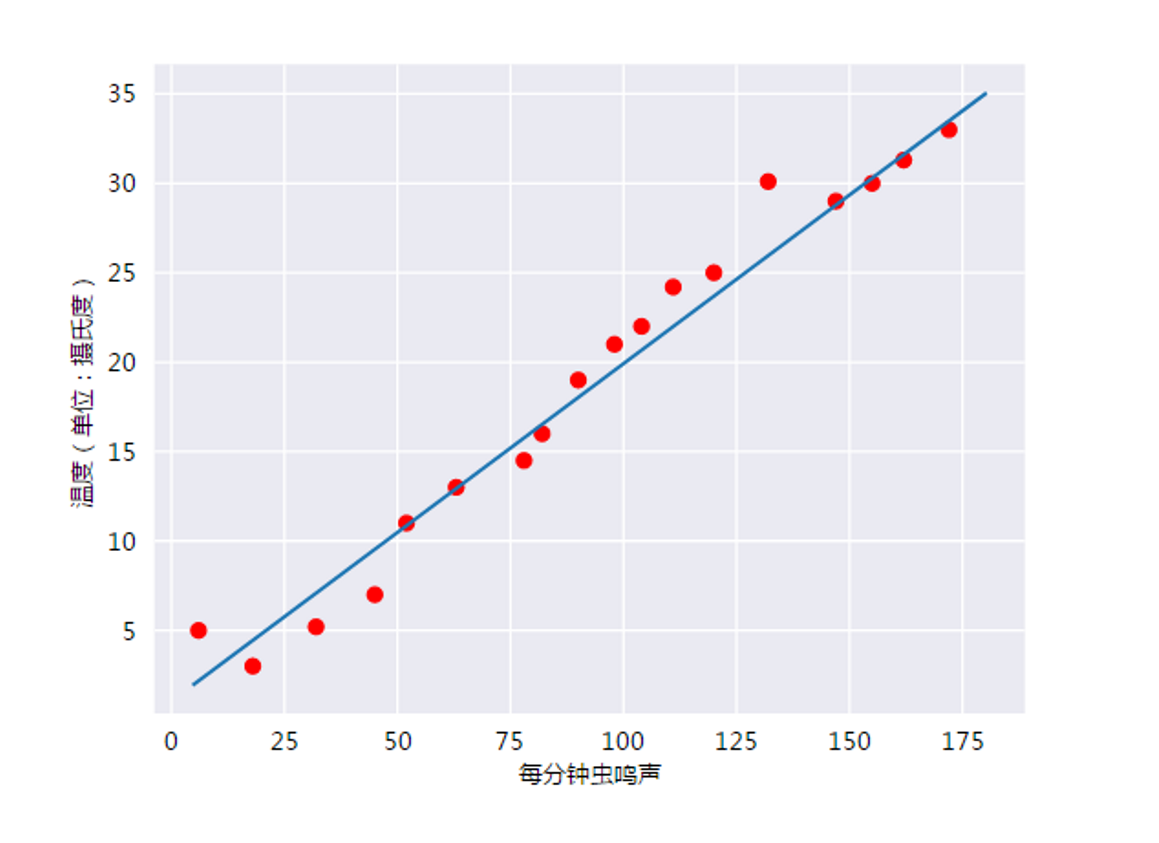
此曲线图表明温度随着鸣叫声次数的增加而上升。我们可以绘制一条直线来近似地表示这种关系，如下所示：

事实上，虽然该直线并未精确无误地经过每个点，但针对我们拥有的数据，清楚地显示了鸣叫声与温度之间的关系(即y = mx + b)。如果我们输入一个新的每分钟的鸣叫声值 x1 推断（预测）温度 y′，只需将 x1 值代入此模型即可。

这个通过已有数据的关系(鸣叫声与温度的关系)，来预测这个线性模型的过程称之为线性回归。

线性回归的实践

下面我们将结合波士顿房价的预测示例，来实际体验在机器学习中如何应用线性回归。

第一步：下载波士顿房价数据

  • 访问https://aistudio.baidu.com/datasetdetail/92436
  • 将boston.csv文件下载到本地juypter notebook目录下

第二步：代码实现

import numpy as np

# 读取boston.csv文件
data = np.genfromtxt('boston.csv', delimiter=',', skip_header=1)

# 分别拆分特征和标签
X = data[:, :-1]  # 特征列
y = data[:, -1]   # 标签列

# 打印特征和标签的形状
print("特征的形状：", X.shape)
print("标签的形状：", y.shape)

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X,
                                                    y,
                                                    test_size=0.15,
                                                    random_state=0)
# KNN
from sklearn.neighbors import KNeighborsRegressor

# 1,构建模型
knn = KNeighborsRegressor()

# 2,训练模型
knn.fit(X=X_train, y=y_train)

# 3,预测
y_pred = knn.predict(X=X_test)

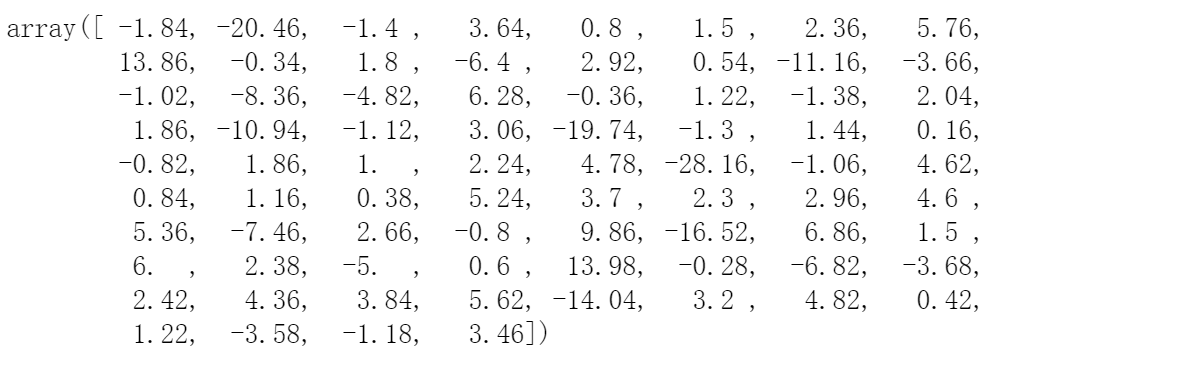
# 4,查看预测结果与真实结果的差别(偏差)
y_pred - y_test

评估指标

分类通常使用准确率、精确度等指标评估模型性能，而线性回归通常使用均绝对偏差、平均平方偏差 等指标评估模型拟合程度。

备注：平均平方偏差不如平均绝对偏差有数据解释性，但是在实际工程中仍然要使用平均平方偏差，因为该值方便求导数。

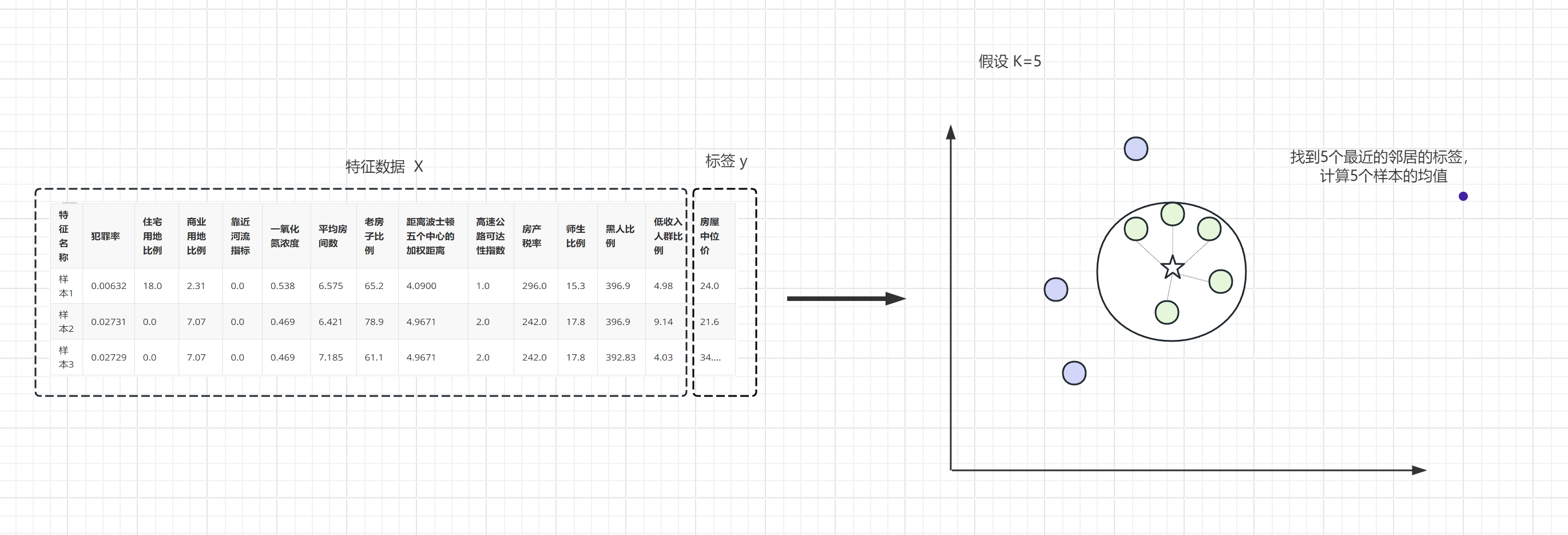
KNN线性回归过程示意

KNN在做分类任务时，是找到最近的K个邻居(例如：K=5)，然后投票选出出现次数最多的类别；线性回归时与分类类似，所不同的是找到最近的K个邻居后，计算它们距离的均值。

除了上述可以使用KNN进行预测之外，也可以使用决策树来预测，代码如下：

# 决策树
from sklearn.tree import DecisionTreeRegressor

# 1,构建模型
dtr = DecisionTreeRegressor()
# 2,训练模型
dtr.fit(X=X_train, y=y_train)
# 3,预测
y_pred = dtr.predict(X=X_test)
# 4,平均绝对偏差
np.abs(y_pred - y_test).mean()

运行结果：

决策树线性回归过程示意

决策树在做分类任务时，找最佳分裂值是通过计算熵(或者gini系数)实现；线性回归与分类过程类似，所不同的是找分裂值时是通过计算方差实现。

有很多的算法都可以用来进行线性回归，在sklearn中也有LinearRegression线性回归可以进行预测，代码如下：

# 线性回归
from sklearn.linear_model import LinearRegression

# 1,构建模型
lr = LinearRegression()

# 2,训练模型
lr.fit(X=X_train, y=y_train)

# 3,预测
y_pred = lr.predict(X=X_test)

np.abs(y_pred - y_test).mean()

运行结果：

线性回归过程示意

  • 输入：X(0 ~ 12)

  • 输出：y

  • 关系：在13维空间内的最简单的函数关系，这个关系又叫线性关系，也叫线性组合或线性回归。

    备注：

    • 由于X与y的关系可以是无穷无尽的，所以再找这两者关系时首先使用的是线性关系，因为这是多个自变量(X)与一个因变量(y)所在空间中最简单的一种关系。
    • 这个关系也叫一层神经网络(感知机层，也叫全连接层、稠密层)，其本质是：参数相乘再相加。

  • 训练过程：把样本数据代入，逐步把权重w（weight）和偏置b（bias）都确定下来。

  • 推理过程：把样本特征X代入确定下来的方程，求解y即可。

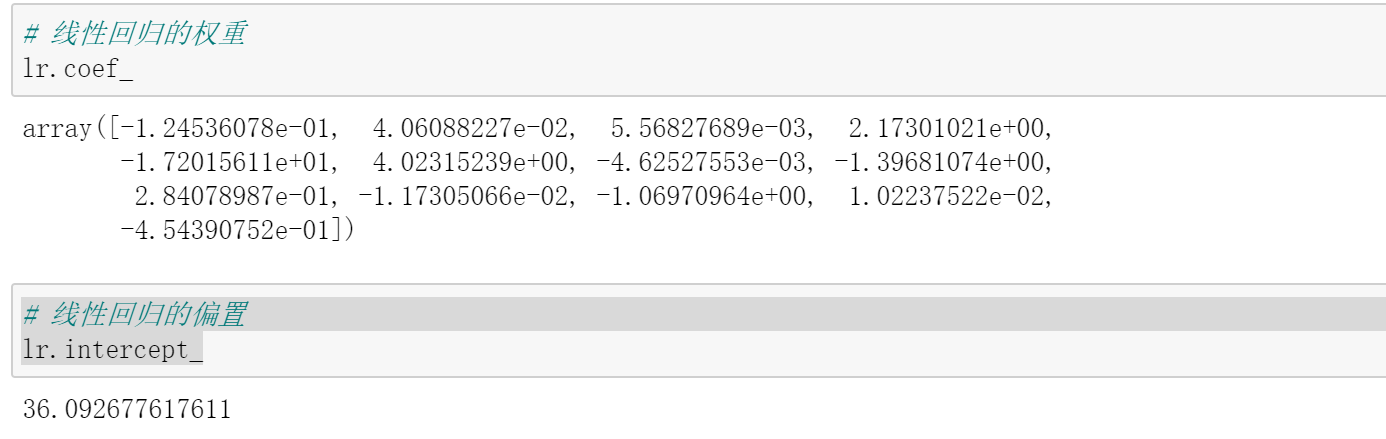
上述w和b可以通过以下方式查看：

# 线性回归的权重
lr.coef_

# 线性回归的偏置
lr.intercept_

逻辑回归

什么是逻辑回归

逻辑回归是一种广义的线性回归分析模型，其核心在于使用Sigmoid函数将线性回归的结果映射到(0,1)的范围内，从而表示属于某一类别的概率。

y=f(x)=sigmod(x_1w_1 + x_2w_2 + ... + x_{13}w_{13} +b)

逻辑回归示例

# 逻辑回归
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split

# 加载乳腺癌数据
X, y = load_breast_cancer(return_X_y=True)

# 切分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, 
                                                    shuffle=True, 
                                                    random_state=0) 
# 1, 构建模型
lr = LogisticRegression( max_iter= 100000)

# 2, 训练模型
lr.fit(X=X_train, y=y_train)

# 3, 评估模型(预测癌症是良性还是恶性)
y_pred = lr.predict(X=X_test)
(y_pred == y_test).mean()

逻辑回归虽然写着是Regression回归，但其本质是二分类，即：通过$sigmod$把任意数转换为[0,1]之间，输出的本质上是0类和1类各自的概率。

特征工程

在上述乳腺癌的示例数据中，其特征值有30个，可以看到特征是比较多的，这里就需要引入特征工程相关的概念。

  • 专业角度：30个特征来自于临床一线专家，每个特征都有医学内涵。
  • 数据角度：30个特征中可能有一些是冗余的。

数据多了可能会导致存储和计算代价增加，所以需要设法消除这些特征。消除冗余特征的方法主要有两类：特征筛选 和 特征降维。

特征筛选

  • 定义：从30个选出重要的来，踢掉不重要的，选出来的是原来30个的一部分。

  • 策略：(如何进行特征筛选)

    • 方式一：随机选择N个(例如：5个)特征，进行准确率分析看哪个结果更好。

    • 方式二：两两判断皮尔逊相关系数，将特征高度相关的列选出来，去掉其中一列。

    • 方式三：利用线性回归的系数来筛选(由于线性回归是相乘再相加，所以系数代表了权重，那么找到权重大的即可)

    备注：利用线性回归是有前提的，需要将数据进行归一化处理。

特征降维

  • 定义：把原来30个特征中的核心信息抽取出来，融合到新生成的N个特征中。(注意：新的特征不是原来的任何一个)
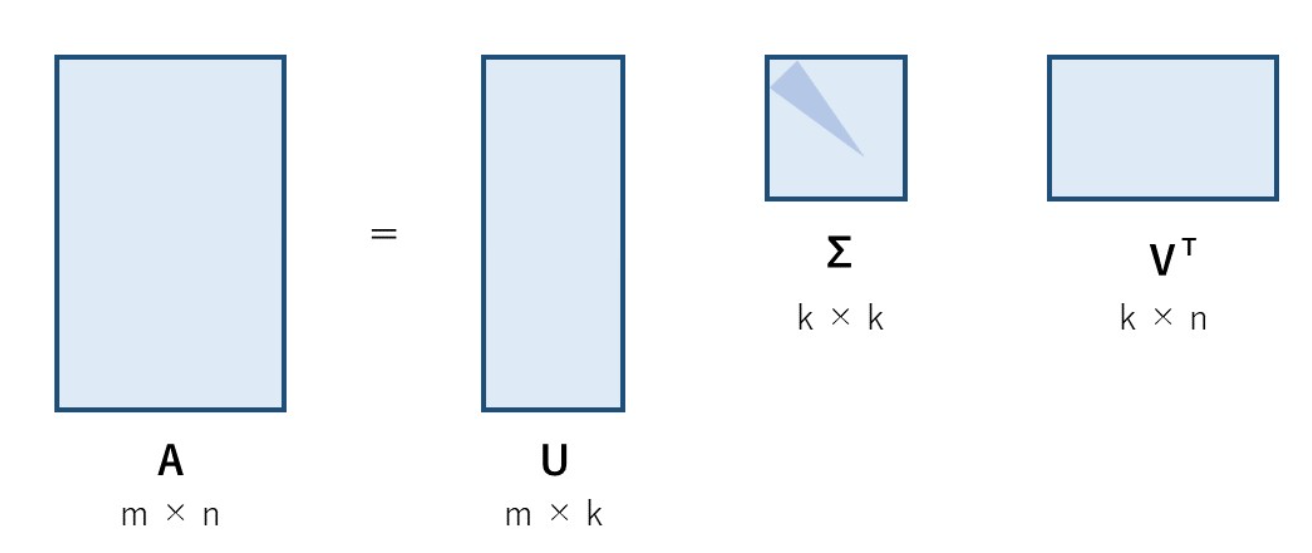
  • 策略：通过SVD分解。

备注：特征降维要比特征筛选更好一些，因为有一些不重要的特征还是有用的，直接去掉是不太合适的。例如：现实生活中一家公司的后勤岗位其重要性相对较低，但是它也是要发挥作用的，缺了谁都不行。

代码实现：

from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split

# 加载乳腺癌数据
X, y = load_breast_cancer(return_X_y=True)

# 切分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, 
                                                    shuffle=True, 
                                                    random_state=0) 
# 特征降维
from sklearn.decomposition import PCA

# PCA:主成分分析，是一种无监督学习
pca = PCA(n_components=20)

# 1, [特征降维]：训练模型
# PCA无监督模型也需要训练，但不需要传入标签
pca.fit(X=X_train)

# 2, [特征降维]：将特征降维至20个(通过X_train1.shape可以查看到特征变为20个)
X_train1 = pca.transform(X=X_train)
X_test1 = pca.transform(X=X_test)

# 3, [逻辑回归]：构建逻辑回归模型
lr1 = LogisticRegression( max_iter= 100000)

# 4, [逻辑回归]：训练逻辑回归模型
lr1.fit(X=X_train1, y=y_train)

# 5, [逻辑回归]：预测评估模型
y_pred = lr1.predict(X=X_test1)
(y_pred == y_test).mean()

运行结果：

为了更加直观看到特征降维后的个数与准确率的关系，我们通过以下代码分别测试30~1个特征的预测准确率，并通过matplotlib的折线图来绘制出曲线：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA

X, y = load_breast_cancer(return_X_y=True)

# 切分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, 
                                                    shuffle=True, 
                                                    random_state=0) 

# 循环测试30~1个特征下的准确率
accuracies = []
num_features = range(30, 0, -1)

for n in num_features:
    pca = PCA(n_components=n)
    pca.fit(X=X_train)
    X_train_pca = pca.transform(X_train)
    X_test_pca = pca.transform(X_test)

    lr = LogisticRegression(max_iter=100000)
    lr.fit(X_train_pca, y_train)

    accuracy = lr.score(X_test_pca, y_test)
    accuracies.append(accuracy)

# 绘制折线图
# 绘制画布
plt.figure(figsize=(10, 6))

# 从特征30开始依次减到0，绘制对应的准确率曲线
plt.plot(range(30, 0, -1), accuracies, marker='o', linestyle='-')

# 绘制X和Y坐标标签以及图标title
plt.xlabel('Number of Features')
plt.ylabel('Accuracy')
plt.title('Relationship between Number of Features and Accuracy')

# 由于显示从30~0，所以对坐标轴进行翻转
plt.gca().invert_xaxis()
plt.grid(True)
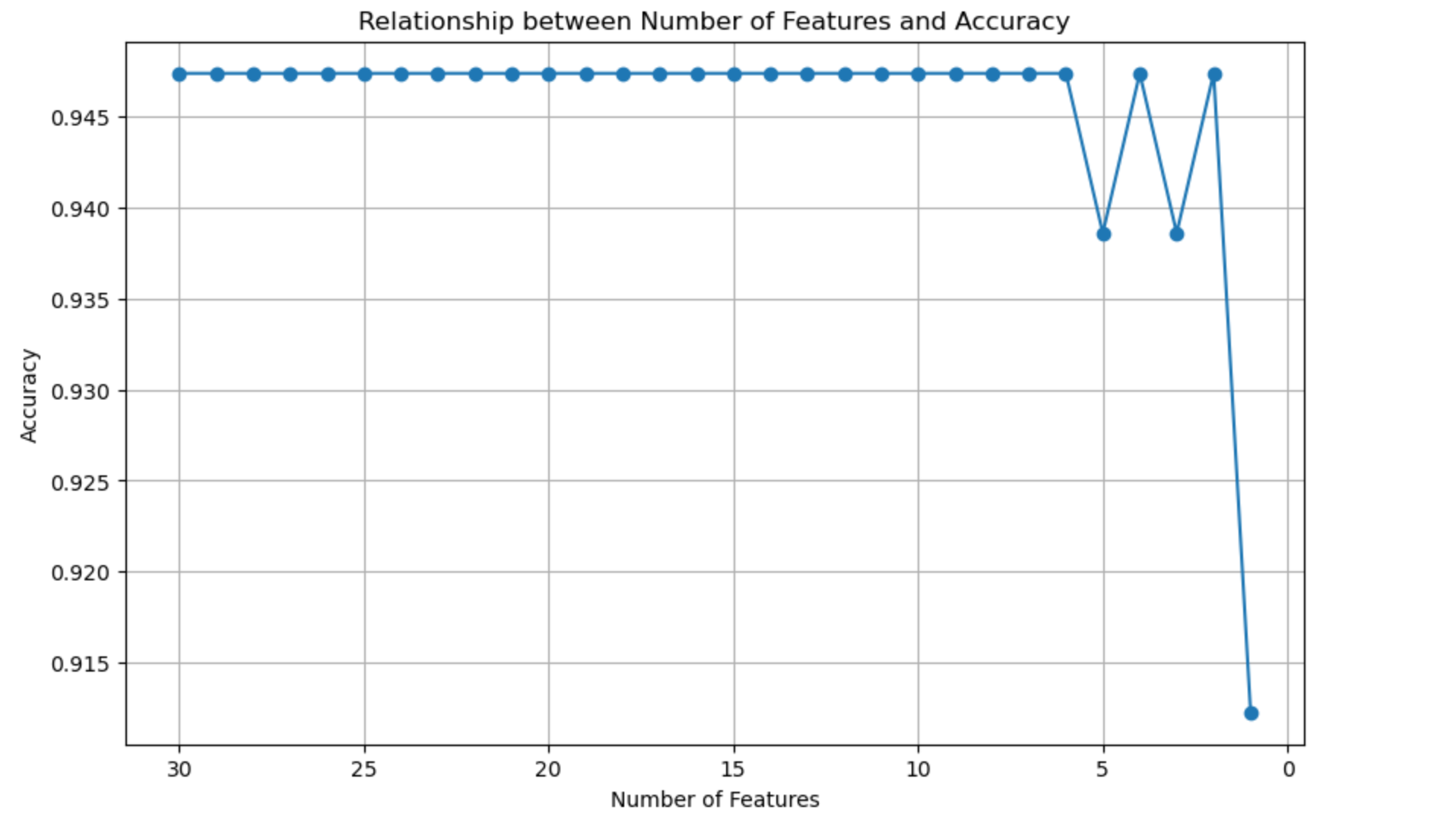
plt.show()

运行结果：

通过上图可以看到，即便特征降维1个，其准确率也没有发生太大变化。这体现了在乳腺癌诊断时业务视角和数据视角不一样的地方：

  • 专业视角：认为30个特征都是很有必要的；

  • 数据视角：认为30个特征是存在非常多的冗余，这会造成不必要的计算代码和存储问题；这30个特征是可以进行特征降维，即便降维1个也不影响准确的。

    备注：但是在解释为什么30个特征能够降维为1个也没有问题时，这个过程不太好解释，这就涉及到SVD分解。

奇异值分解（SVD）

核心思想

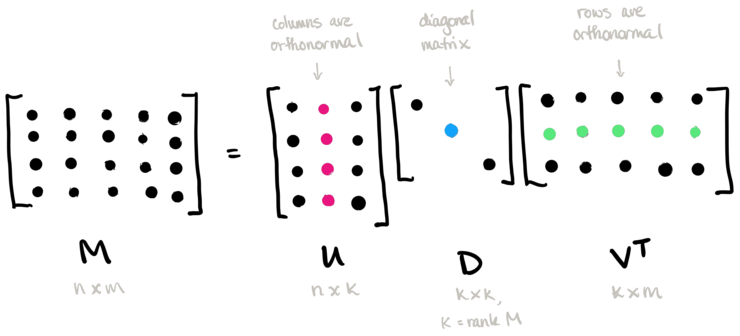
  • 奇异值分解可以将一个比较复杂的矩阵，用更小更简单的几个子矩阵的相乘来表示，这些小矩阵描述的是矩阵的重要的特性。

    就像是描述一个人一样，给别人描述说这个人长得浓眉大眼，方脸，络腮胡，而且带个黑框的眼镜，这样寥寥的几个特征，就让别人脑海里面就有一个较为清楚的认识。

由于SVD涉及到线性代数中基础知识，所以其数学推导原理较难理解(想了解详情可以查看b站视频：【代数明珠–奇异值分解（SVD）生动动画演示！】)。

奇异值分解直观应用(女神压缩)

为了对奇异值分解有一个直观认识，接下来将通过对美女图片使用SVD分解进行图片压缩，具体操作步骤：

第一步：找一张美女的图片，保存到代码相同目录。

例如：我们从搜索引擎搜索美女，保存对应的图片到本地并命名为beautiful.jpg

第二步：在Jupyter notebook中读取图片并打印图片相关信息

import numpy as np 
from matplotlib import pyplot as plt

# 读取
beauty = plt.imread(fname="beautiful.jpg")

# 输出图片信息(高度、宽度、通道)
beauty.shape

运行结果：

这是一张高度621*宽度917的图片，有3个通道

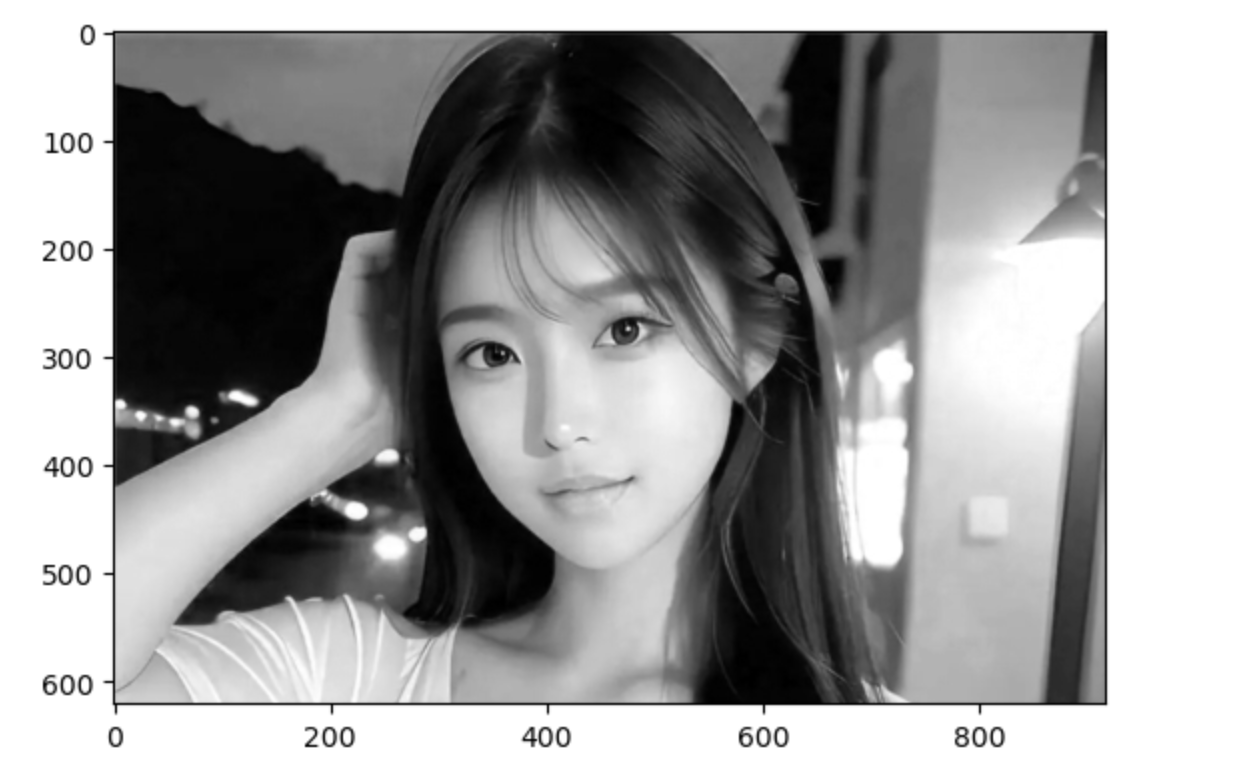
第三步：显示R通道的内容

# 抽取图片的R通道并现实
r = beauty[:, :, 0]
plt.imshow(X=r, cmap="gray" )

运行结果：

第四步：对图片(图片信息本质是一个矩阵)进行SVD分解

# SVD分解：将一个复杂的矩阵()
U, S, V = np.linalg.svd(a=r, full_matrices=False)

print('原始图片，即r矩阵：', r)

print('左奇异矩阵：', U)
print('右奇异矩阵：', V)
print('奇异值：', S)
print('奇异值转变为对角线矩阵：', np.diag(S))

# 因为r = U @ np.diag(S) @ V
print('U、np.diag(S)、V矩阵相乘:', U @ np.diag(S) @ V)
  • 通过对比原始矩阵r和U @ np.diag(S) @ V的结果，两者是一致的。
  • 含义：将一个复杂的矩阵(原始图片r)，分解为三个简单的矩阵相乘。
    • U：左奇异矩阵
    • V：右奇异矩阵
    • S：奇异值，一串大于0的正数
    • np.diag(S)：将奇异值转变为一个对角线矩阵

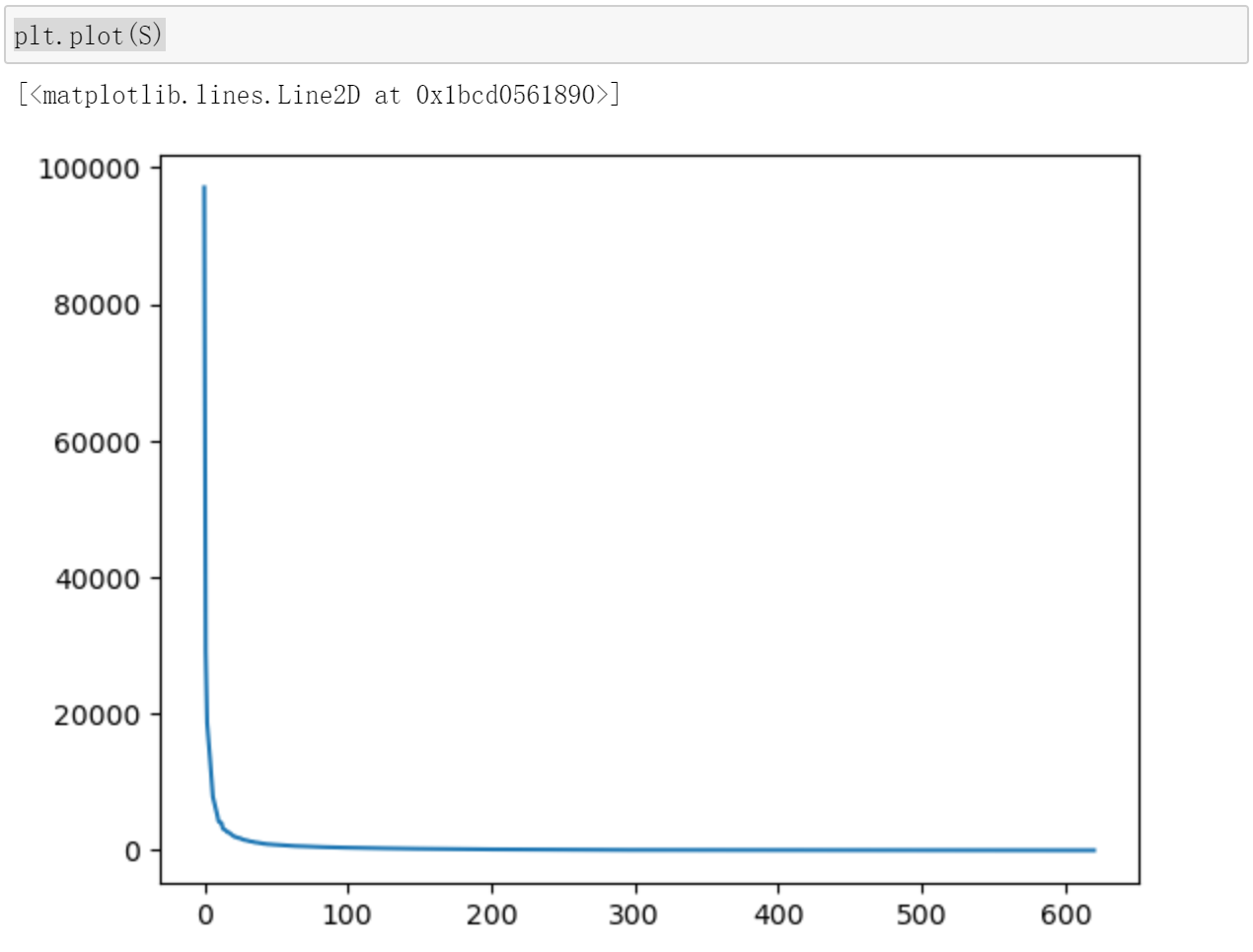
第五步：查看奇异值

该图片代表从左往右，奇异值的重要性，只有前面几个奇异值是有用的，后面的奇异值没什么用。

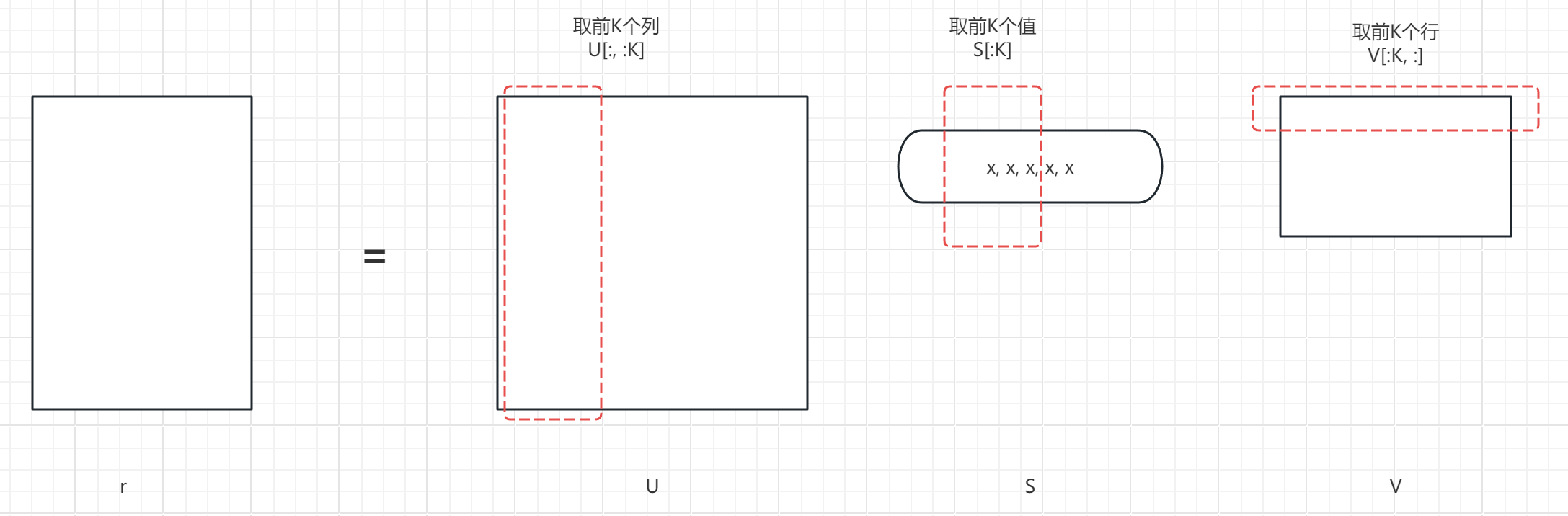
第六步：女神图片压缩

我们分别取U的前K个列数据，S的前K个值，V的前K个行。(保持一致才能矩阵相乘)

# 设置要取的奇异值个数
K = 100

# 分别从U中取前K列，V中取前K行，S中前K值，矩阵相乘保存到result
result = U[:,:K] @ np.diag(S[:K]) @ V[:K,:]

# 绘制乘积后矩阵
plt.imshow(X=result, cmap="gray" )

运行结果：

可以看到女神的图片信息并没有太多的损失。

进一步：为了看到奇异值筛选个数对图片的影响，我们分别选取前100个奇异值、前50个、前10个、前5个奇异值并绘制图片，对比其显示结果，代码如下：

import numpy as np
from matplotlib import pyplot as plt

# 读取图片
beauty = plt.imread(fname="beautiful.jpg")

# 提取R通道
r = beauty[:, :, 0]

# 进行SVD分解
U, S, V = np.linalg.svd(a=r, full_matrices=False)

# 设置选取100, 50, 10 , 5 四个奇异值数据
singular_values = [100, 50, 10, 5]

# 绘制五个子图以便放在一个画布上显示
fig, axs = plt.subplots(1, len(singular_values)+1, figsize=(20, 5))

# 绘制原始图片
axs[0].imshow(X=r, cmap="gray")
axs[0].set_title('Original Image')

# 依次绘制100, 50, 10, 5奇异值下的图片
for i, k in enumerate(singular_values):
    result = U[:, :k] @ np.diag(S[:k]) @ V[:k, :]
    axs[i+1].imshow(X=result, cmap="gray")
    axs[i+1].set_title(f'Singular Values: {k}')

# 显示画布
plt.show()

运行结果：

可以看到当奇异值取前10个的时候，图片已经模糊；取前5个时，基本只能看出一个轮廓了。

聚类算法

KMeans算法

问题场景

假设有这样一个电商大数据推荐场景，某App在618要进行促销活动，该应用的用户群体有1000万。这1000万用户大致可以分为三类：

  • 分类一：死忠粉丝群体。这类群体在促销活动中不做任何降价(因为他们是死忠粉丝，多少钱都愿意买)
  • 分类二：摇摆派群体。关注商品的性价比，谁家的东西便宜买谁的。这类群体给予一定的优惠，把他们吸引过来。
  • 分类三：潜在群体。这类用户使用的是竞品产品，是潜在可以拉拢过来的用户，需要给予更大力度的优惠。

问题：如何将这三类用户分类出来？

代码实现

以上是一个典型的聚类算法要解决的问题，接下来通过代码来实现。

from sklearn.datasets import make_blobs
from matplotlib import pyplot as plt

# 生成2000个假数据
# n_features=2，代表每个数据有2个特征
# centers=5，数据有5个中心
# cluster_std=0.5，设置假数据的标准差，使得数据更加集中
X, y = make_blobs(n_samples=2000, 
                  n_features=2,
                  centers=5,
                  random_state=0,
                  cluster_std=0.5)

# 将数据绘制到散点图里
plt.scatter(X[:,0], X[:,1], c=y)

# 引入KMeans模型
from sklearn.cluster import KMeans

# 1, 构建模型
km = KMeans(n_clusters=5, n_init="auto")

# 2, 训练模型
km.fit(X=X)

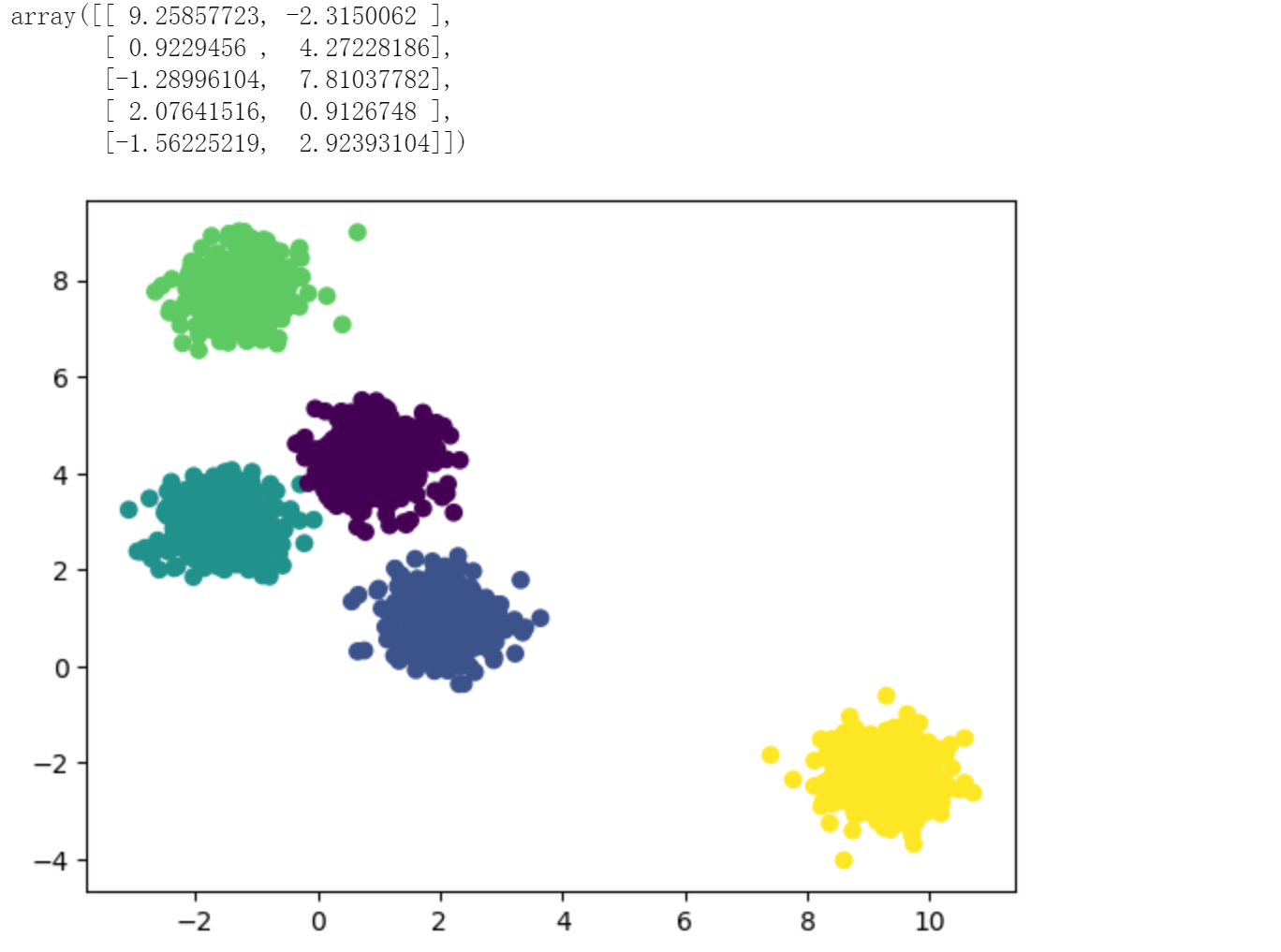
# 3, 打印找到的分类中心
km.cluster_centers_

运行结果：

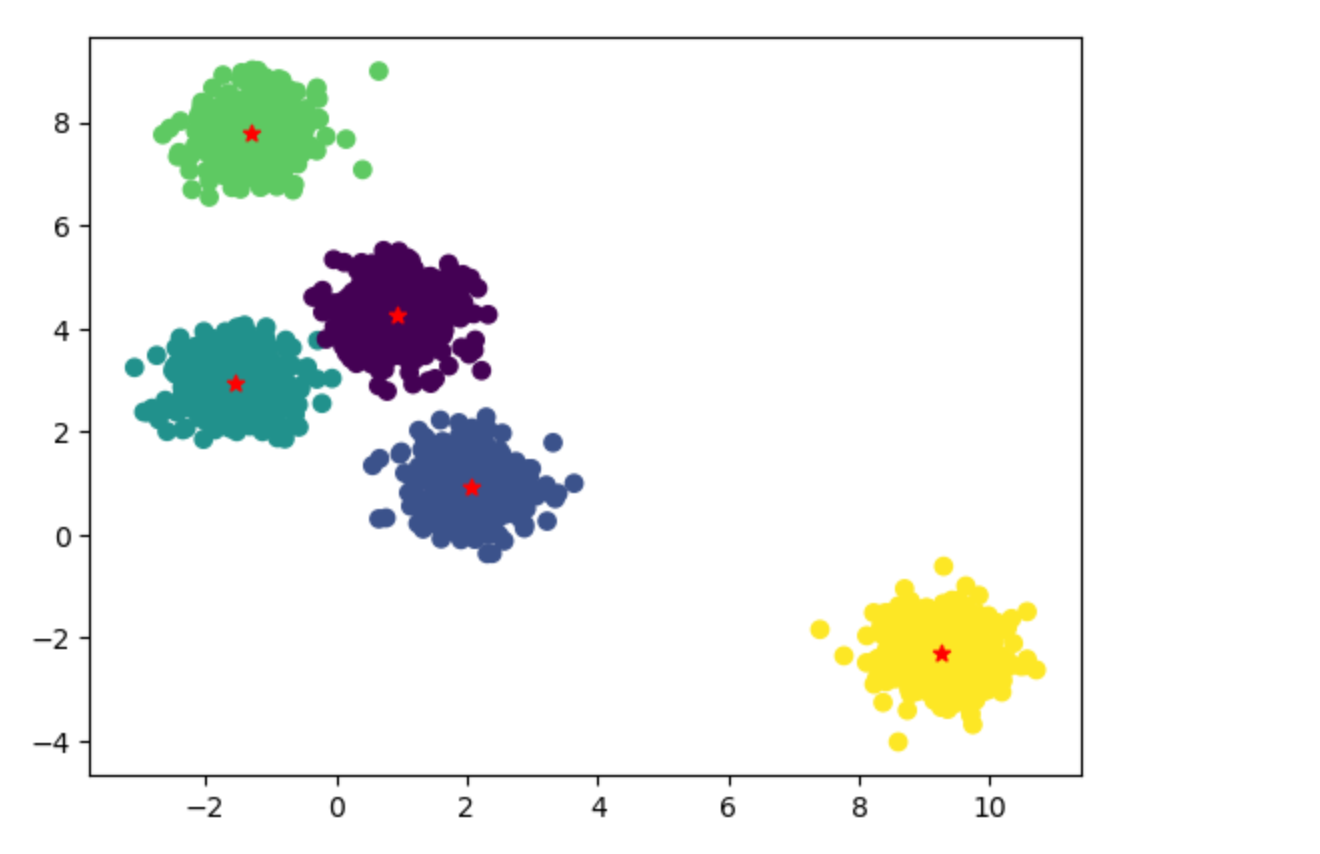
# 绘制原始数据散点图
plt.scatter(X[:,0], X[:,1], c=y)

# 绘制分类中心使用红色五角星显示
plt.scatter(km.cluster_centers_[:,0], km.cluster_centers_[:,1], marker="*", c='red')

通过以上图示可以看到，通过Kmeans算法找到了5个分类中心。

这里由于假数据是我们指定生成了5个分类中心数据(属于拥有上帝视角)，所以觉得很容易可以找到5个分类中心。实际工程应用中没有上帝视角，那么找到5个分类中心还是不容易的，需要使用迭代法。

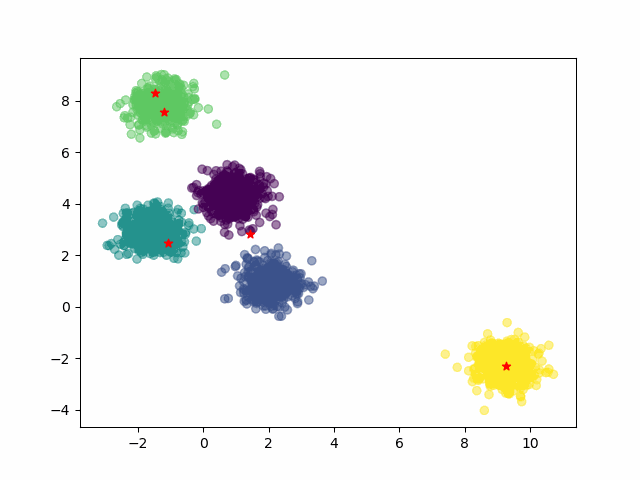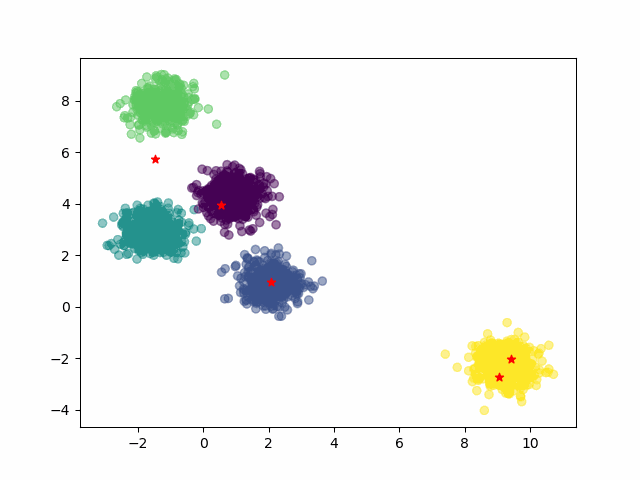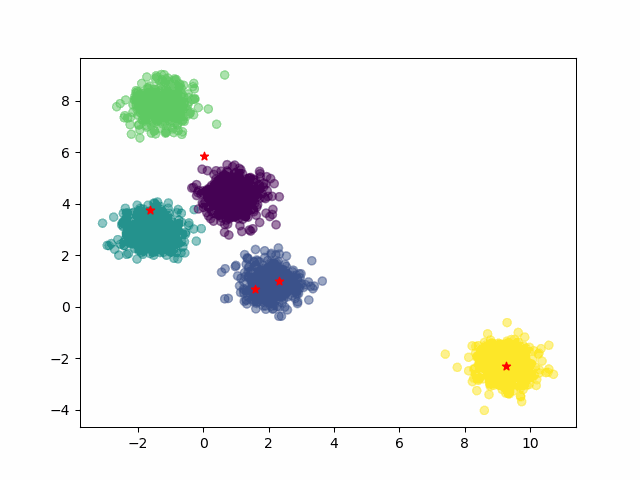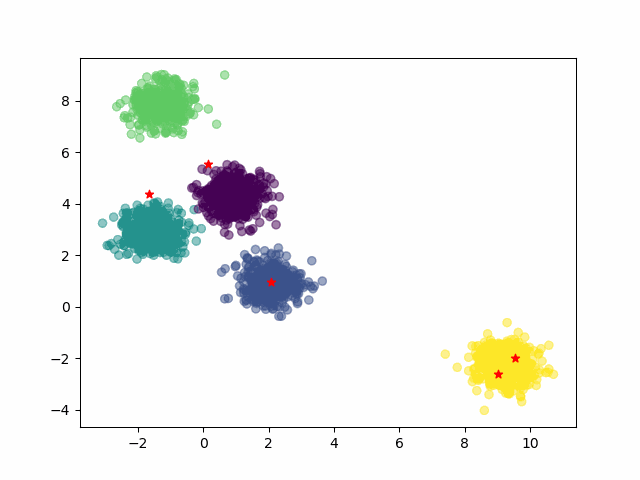
迭代法

定义：迭代法是一种通过反复迭代逼近问题解的方法，通过多次重复执行相同的计算步骤，逐步逼近问题的解。

核心思想："先粗糙的开始，然后慢慢地变好"

步骤：

  • 从一个随机状态开始
  • 采用一定的策略，逐步变好
  • 从量变达到质变的过程
  • 最后实现目的

举个生活中的例子理解上述步骤：

  • 随机抽取两个班长，一个正班长，一个副班长
  • 一个月后再次重新选，投票制
  • 两个月后再次选班长
  • 每半年选一次班长
  • ….
  • 新选的班长与上次的班长一样，结束

…..如此迭代，选择的班长一定是合理。

启发："事上练"的道理与迭代法不谋而合。我们不论做什么事情，要先行动起来，在实践的过程中不断优化和改进。

人工智能补充知识

机器学习中的任务分类

任务分类 数据特点 预测问题类型
有监督学习 (Supervised) 有特征和标签，用于分类和回归问题 分类问题(Classification)：预测离散量
回归问题(Regression)：预测连续量
无监督学习 (Unsupervised) 有特征但没有标签，用于聚类和降维算法 聚类问题：KMeans
降维问题：PCA
自监督学习 (Self-Supervised) 大模型预训练时使用自监督，输入文本自我挖空填空 –

人工智能技术三次高潮

  • 第一代技术：机器学习
  • 第二代技术：深度学习
  • 第三代技术：大模型技术

集成学习

集成学习定义

集成学习（Ensemble Learning）是一种机器学习方法，通过结合多个基础模型的预测结果来提高整体模型的准确性和稳定性。

集成学习核心思想

  • 集成学习的核心思想是“三个臭皮匠顶个诸葛亮”，即通过组合多个弱分类器或回归器，最终得到一个强分类器或回归器，以提高预测性能。
  • 集成学习也是一种头脑风暴的思想，即让不同意见的人提出不同的意见，最后选一个更好的。

集成学习的方法

集成学习有多种方法：

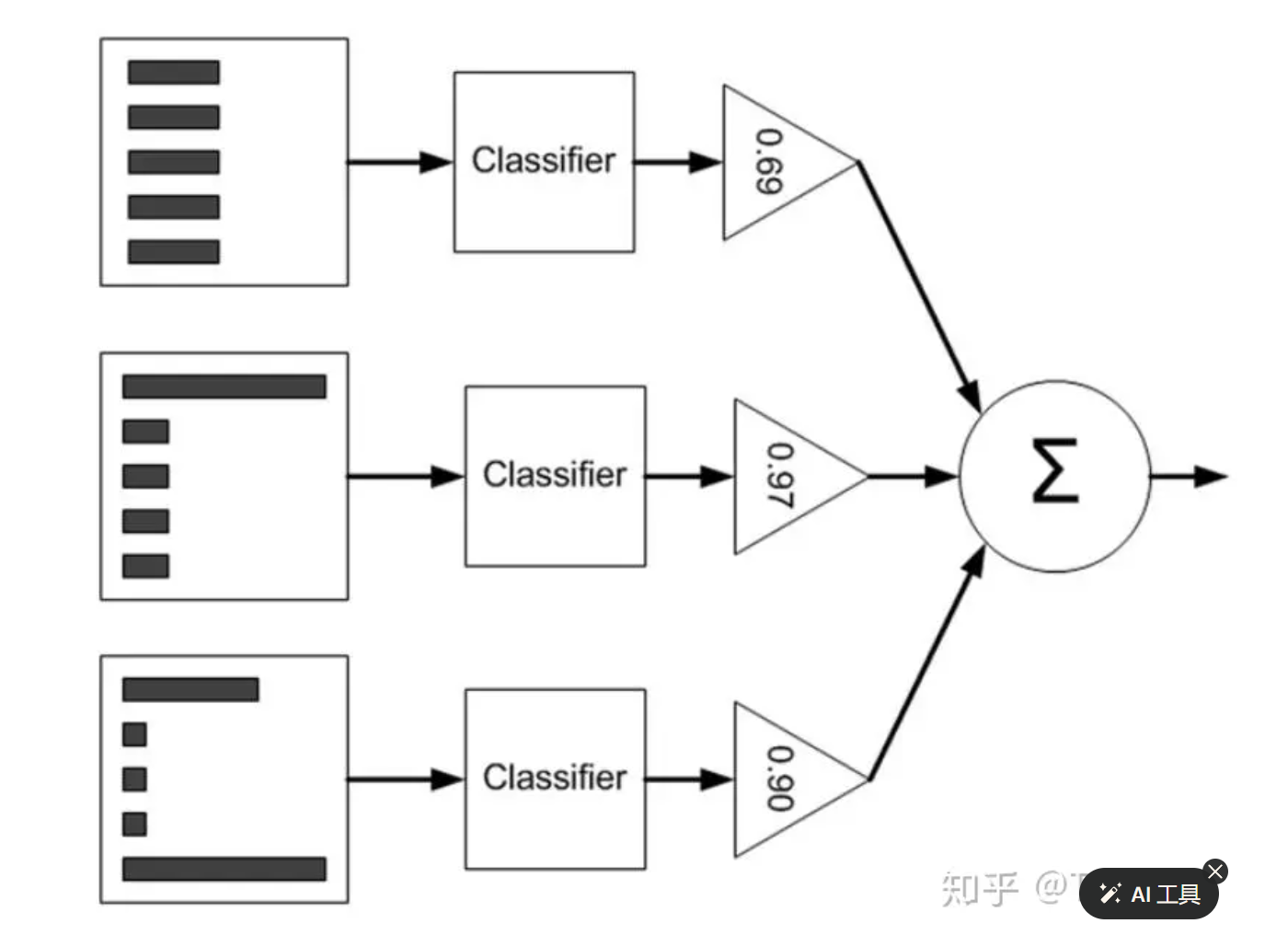
  • Voting：通过结合多个基础模型的预测结果来提高整体模型的准确性和稳定性。
    • 硬投票（Hard Voting）：在硬投票中，每个基础模型投票选择出现次数最多的类别作为最终的预测结果。对于分类问题，硬投票是常用的方法。
    • 软投票（Soft Voting）：在软投票中，每个基础模型的预测结果被加权平均，得到概率最高的类别作为最终的预测结果。对于分类问题和概率估计问题，软投票通常比硬投票更有效。
  • Bagging：通过并行训练多个基础模型，每个模型使用不同的子样本进行训练，然后将它们的预测结果进行平均或投票来得到最终预测结果。常见的Bagging算法包括随机森林（Random Forest）。
  • Boosting：通过串行训练多个基础模型，每个模型都尝试修正前一个模型的错误，最终组合多个模型以得到更准确的预测结果。常见的Boosting算法包括Adaboost、Gradient Boosting和XGBoost。

集成学习的实践

Voting方法

from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 加载鸢尾花数据集
iris = load_iris()
X, y = iris.data, iris.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 初始化三个基础分类器：逻辑回归、决策树、支持向量机
clf1 = LogisticRegression()
clf2 = DecisionTreeClassifier()
clf3 = SVC(probability=True)

# 创建VotingClassifier，使用硬投票策略
voting_clf = VotingClassifier(estimators=[('lr', clf1), ('dt', clf2), ('svm', clf3)], voting='hard')

# 训练VotingClassifier模型
voting_clf.fit(X_train, y_train)

# 预测并计算准确率
y_pred = voting_clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print("VotingClassifier模型的准确率：", accuracy)

Bagging方法

from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 加载鸢尾花数据集
iris = load_iris()
X, y = iris.data, iris.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 初始化基础分类器为决策树
base_classifier = DecisionTreeClassifier()

# 创建BaggingClassifier
bagging_clf = BaggingClassifier(base_estimator=base_classifier, n_estimators=10, random_state=42)

# 训练BaggingClassifier模型
bagging_clf.fit(X_train, y_train)

# 预测并计算准确率
y_pred = bagging_clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print("BaggingClassifier模型的准确率：", accuracy)

在这个示例中，我们使用Bagging方法构建了一个BaggingClassifier，基础分类器为决策树，并训练了一个包含10个基础分类器的Bagging模型。最后，输出了BaggingClassifier模型的准确率。

Stacking方法

from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import StackingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification

# 创建一个示例数据集
X, y = make_classification(n_samples=1000, n_features=20, n_informative=10, n_classes=2, random_state=42)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 定义基础模型
base_models = [
    ('rf', RandomForestClassifier(n_estimators=100, random_state=42)),
    ('gb', GradientBoostingClassifier(n_estimators=100, random_state=42))
]

# 定义次级模型
meta_model = LogisticRegression()

# 创建Stacking集成模型
stacking_model = StackingClassifier(estimators=base_models, final_estimator=meta_model)

# 训练Stacking模型
stacking_model.fit(X_train, y_train)

# 在测试集上进行预测
y_pred = stacking_model.predict(X_test)

# 输出准确率
accuracy = stacking_model.score(X_test, y_test)
print(f"Stacking模型的准确率：{accuracy}")

在这个示例中，我们使用了随机森林（Random Forest）和梯度提升树（Gradient Boosting）作为基础模型(第一阶段)，逻辑回归作为次级模型(第二阶段)，构建了一个Stacking集成模型。

集成学习的对比

集成学习方法 准确率 召回率 推理速度 训练速度
随机森林 高 中 中等 中等
KNN 中 高 快 慢
高斯贝叶斯 低 低 快 快
决策树 中 中 快 快
支持向量机 高 高 慢 慢

随机森林

随机森林是一种集成学习方法，它通过构建多个决策树并结合它们的预测结果来提高整体预测准确性。以下是随机森林的主要过程：

  • 随机抽样：

    • 从训练集中随机选择一部分样本(样本级随机，也叫行级随机)，用于构建每棵决策树的训练集。这种随机抽样保证了每棵决策树的训练集是不同的。
      特征

  • 随机选择：

    • 在每次节点划分时，随机选择一部分特征作为候选特征(特征级随机，也叫列级随机)。这样可以增加决策树的多样性，避免过拟合。

  • 决策树的构建：

    • 对于每棵决策树，根据选定的特征和样本，通过递归地选择最佳特征和划分点来构建树结构，直到满足停止条件（如达到最大深度、节点样本数小于阈值）为止。

  • 预测结果整合：

    • 对于分类问题，随机森林通过投票方式（多数表决）来整合每棵树的预测结果；对于回归问题，取平均值作为最终预测结果。

内容小结

  • 线性回归

    • 分类问题预测数据所属的类别，而线性回归预测连续数值输出。
    • 线性回归通常使用均绝对偏差、平均平方偏差 等指标评估模型拟合程度

  • 逻辑回归

    • 逻辑回归是一种广义的线性回归分析模型，其核心在于使用Sigmoid函数将线性回归的结果映射到(0,1)的范围内。

  • 特征工程

    • 特征数据处理时，可能存在冗余的情况，这会增加存储和计算代价。消除冗余特征的方法主要有两类：特征筛选 和 特征降维。
    • 特征降维要比特征筛选更好一些，因为有一些不重要的特征还是有用的，直接去掉是不太合适的。
    • 特征降维主要使用奇异值分解，将一个比较复杂的矩阵，用更小更简单的几个子矩阵的相乘来表示。

  • 聚类算法

    • 迭代法是一种通过反复迭代逼近问题解的方法，通过多次重复执行相同的计算步骤，逐步逼近问题的解。

  • 集成学习

    • 集成学习（Ensemble Learning）是一种机器学习方法，通过结合多个基础模型的预测结果来提高整体模型的准确性和稳定性。
    • 集成学习的核心思想是“三个臭皮匠顶个诸葛亮”。
    • 集成学习有多重方法，其中随机森林在性能指标、推理速度、训练速度方面表现最好。

参考资料：

线性回归

线性回归算法原理与总结

【代数明珠–奇异值分解（SVD）生动动画演示！】

知乎：奇异值的物理意义是什么？

知乎：奇异值分解（SVD）

欢迎关注公众号以获得最新的文章和新闻

发表评论

您的邮箱地址不会被公开。 必填项已用 * 标注

分类文章

personal_logo
Dongming
自由职业者

推荐活动

推荐文章

【操作攻略】GPU云环境的使用介绍
2024-11-14
1 week ago
【项目实战】通过LLaMaFactory+Qwen2-VL-2B微调一个多模态医疗大模型
2024-10-27
3 weeks ago
【课程总结】day19（中）：Transformer架构及注意力机制了解
2024-08-02
3 months ago
【重拾数学知识】矢量的点乘和叉乘
2024-10-18
1 month ago
【课程总结】Day11（上）：手势图像识别实战(LeNet模型)
2024-06-24
4 months ago
【课程总结】day34：多模态大模型之ViT模型、CLIP模型论文阅读理解
2024-10-14
1 month ago
【目录】AI知识学习路线图
2024-05-21
6 months ago
【课程总结】day33：文生图StableDiffusion模型初步了解以及部署体验
2024-10-13
1 month ago
【课程总结】day32(下)：Xinference部署向量化模型
2024-10-10
1 month ago
【课程总结】day31：多模态大模型初步了解
2024-09-30
1 month ago
菜单

文章目录

→ 内容目录
滚动至顶部